뽀또12

인공지능을 공부하는 사람들하고 많은 지식을 공유하고, 제가 아는 것을 많이 알려드리고 싶습니다.

정말 하고 싶은게 너무 많아요. 모두들 항상 즐겁고 행복하게 열심히 삽시다! 오늘도 파이팅입니다!

업데이트:

카테고리:

데이터 타입

데이터는 크게 카테고리형과 수치형의 2가지 종류의 특징이 있습니다.

  • 카테고리형 : 남/녀, 집이 있음/없음, 1등급/2등급/…/N등급
  • 수치형 : 온도,날짜,수량,나이 등 수치적인 값

음.. 카테고리형은 분류 모델에 적용할 것 같고, 수치형은 회귀 모델에 적용할 것 같이 보이네요!

값에 따라서 discrete/continuous로 구분할 수 있는데, 카테고리형처럼 딱딱 나눠지는 것을 discrete, 수치형처럼 연속적인 값을 갖는 것을 continuous하다고 볼 수 있습니다.



데이터 집합의 일반적인 특징

  • Dimensionality

    훈련 데이터들이 N차원의 특징들을 갖고 있다고 해봅시다. 그럼 각각의 데이터들은 N차원의 공간에서 하나의 점으로 표현됩니다.

    3차원을 예로 들어봅시다. 데이터가 1000개 있다고 하면, 어떻게 보면 되게 데이터가 꽤 있다고 볼 수 있습니다. 그러나 3차원의 각 축이 1~100의 범위를 가진다고 해봅시다. 그러면 해당 데이터가 존재할 3차원의 공간은 $100^3$의 점들을 가질 수 있습니다. 그럼 우리가 가진 데이터는 3차원의 공간에서 $ 1000/(100\times100\times100)=1/1000$ 즉 0.001%만 사용하고 있는겁니다. 3차원이라서 다행이지 10차원이었다면 어땠을까요? 이렇듯 고차원으로 갈수록 차원의 저주는 심각해집니다. 차원의 저주가 심해지면, 우리가 갖고 있는 데이터가 전체 데이터를 대표하는 표본인지 알 수 없게 됩니다.

    이것은 고차원으로 갈수록 점점더 심해집니다. 이를 우리는 차원의 저주(curse of dimensionality)라고 부르고, 이것이 차원 감소(dimensionality reduction)이 데이터 전처리에 한 축이 되는 이유입니다.

  • Distribution

    데이터들의 집합이 어떤 분포를 이룰 때가 있습니다. 그럴 땐 분포를 모델링해서 강력한 분석 기법을 적용할 수 있습니다. 그러나, 실제 데이터들은 우리가 아는 통계 분포들로 표현하기 어려울 때가 많습니다. 따라서 많은 데이터 마이닝 알고리즘들은 데이터에 대해 특정한 통계 분포를 가정하진 않습니다.

  • resolution

    데이터는 다들 다른 범위의 값을 가집니다. 따라서 해상도를 어떻게 조절하느냐에 따라서, 우리는 데이터의 전반적인 패턴을 파악할 수 있냐 없냐로 나뉘는 경우가 종종 있습니다. 예를 들면, 일주일 동안 기상상황을 본다고 해봅시다. 7일 중 비가 하루만 오고 낮에 날씨가 선선했습니다. 그럼 우리는 지금의 계절을 가을이라고 예측하게 될까요? 봄이라고 하게 될까요? 이제 날씨를 1개월 단위로 봐봅시다. 12개월중 유독 6,7월에 기온이 높습니다. 그럼 우리는 아, 6,7월엔 적어도 여름이겠구나 파악할 수 있는 겁니다.

    따라서 데이터를 어떻게 갖고 노느냐에 따라 우리는 더 좋은 학습을 이뤄낼지도 모릅니다.



데이터 품질

  • 잡음(noise)

    예제
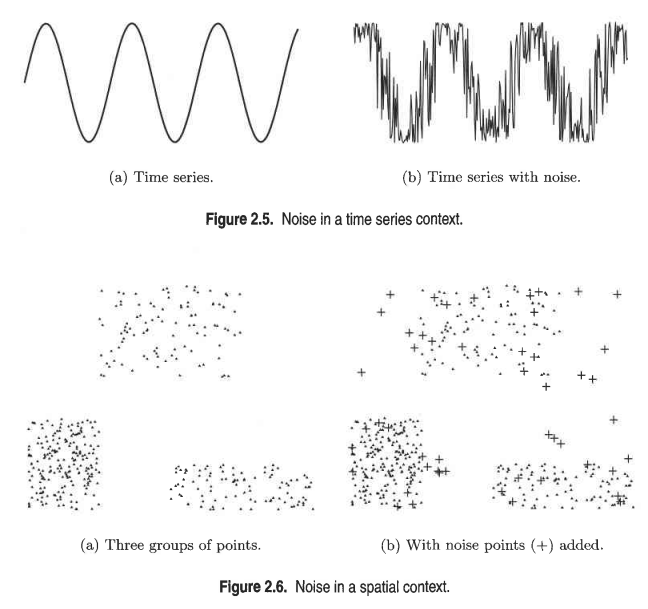
    잡음 예시

    데이터는 잡음(noise)이 있을 수 있습니다. 그래서 우리는 잡음을 항상 고려하는 robust algorithm을 적용하려고 노력해야합니다.

  • 정밀도,편차

    데이터는 결국 기기로 측정되는 경우가 많습니다. 기기가 값싼 장비일수록 정밀한 측정이 불가능할 때도 있을 것이고, 이에 따라 매번 측정하는 값이 바뀌니 편차도 생길 것입니다. 이런 것도 항상 고려해야할 것입니다.

  • 이상치(outlier)

    데이터가 가끔 팍! 하고 튀어서 이상한 값이 나올 수 있습니다. 극단적인 예로, 평균 키가 170인 일반인들이 있는 곳에 서장훈씨가 있다고 해봅시다. 그럼.. 안봐도 뭔가 이상하지요? 이럴 경우엔 보통 서장훈씨를 이상치라고 볼 수 있습니다.

  • 누락 값(missing value)

    말 그대로 데이터에서 특징 값이 누락된 경우가 있을 수 있습니다. 이럴 땐 여러 가지 처리법이 있는데 간단히 3개정도만 언급하겠습니다.

    • 데이터 객체 또는 특징을 제거 : 누락된 값이 있는 데이터를 지우던지, 아니면 특징을 아예 지워버리기
    • 누락 값을 추정 : 다른 데이터들의 같은 특징들을 이용해서 평균 값으로 채워넣는 등의 방법
    • 분석 과정에서 누락 값을 무시 : 누락값의 수들이 많지 않거나, 특징들의 수가 적지 않다면 그냥 누락 값 자체를 사용하지 않고 분석하는 것



데이터 전처리

데이터 전처리는 데이터를 데이터 마이닝에 적합하게 만들기 위해 전처리를 하는 것을 목표로 합니다. 방법에는 여러가지가 있습니다. 간략히 살펴봅시다.

  • Aggregation

    이것은 2개 이상의 데이터들을 하나의 데이터로 결합하는 것을 의미합니다. 간단한 예로 날짜를 예를 들어봅시다. 날짜라는 특징은 365일을 dicrete하게 값을 갖습니다. 날짜(일) 데이터로 학습을 하게 되면 데이터들의 패턴이 각각 따로 노는 것처럼 보일 수 있습니다. 이걸 다 합쳤다가 12개월로 다시 쪼개는 겁니다. 그럼 각 월마다의 어떤 패턴이 보일지도 모릅니다.

  • 표본 추출(sampling)

    데이터가 너무 많을 경우, 전제 데이터를 학습에 사용하는 것은 효율적이지 않습니다. 그럴 때, 이 데이터 셋을 대표하는 부분집합으로 학습을 한다면 어떨까요? 전체 데이터를 충분히 대표할 수 있는, 즉 표본이 대표적이라면 표본을 학습에 사용해도 전체 데이터를 사용하는 것과 같은 효과를 볼 수 있습니다.

    예제
    표본 추출 예시

    위 그림은 표본 추출의 예시를 보여줍니다. 전체 데이터 셋은 (a)입니다. 무려 8천개의 포인트 셋이죠. 이걸 다 학습에 사용하면 많은 배치를 돌아야 할 것입니다. 그러나, 이 데이터들을 대표하는 부분집합을 (b)처럼 추출해서 학습을 하면 (a)를 이용하는 것과 비슷한 학습 효과를 볼 수 있습니다. 단, 너무 적은 데이터셋을 뽑게 되면 (c)처럼 데이터의 패턴을 읽게 됩니다.

    그럼 적절한 표본의 크기는 몇일까요? 이건 한번에 알아볼 수 없습니다. 그래서 adaptive/progressive 표본 추출 기법이 사용됩니다. 순서는 다음과 같습니다.

    1. 표본을 적게 추출한다.
    2. 학습한다.
    3. 정확도를 본다.
    4. 표본의 수를 늘린다.
    5. 2~4를 반복하다가 정확도가 더 이상 증가하지 않는 지점에서 멈춘다. 이 때의 표본 수가 적절한 표본 수이다.

  • 차원 축소(dimensionality reduction)

    차원의 저주는 고차원으로 갈수록 심각해짐을 위에서 살펴봤었습니다. 특히 문서 데이터를 벡터화한 테이블이 있다고 해봅시다.. 많은 특징들이 존재하게 될텐데.. 차원의 저주가 매우 심각하겠지요. 그래서 차원을 축소하여 이를 해결합니다. 차원 축소를 위한 기법은 가장 유명한 것이 주성분 분석(Principal Component Analysis)와 특이값 분해(Singular Value Decomposition)입니다. 해당 내용들은 후에 따로 정리하겠습니다.

  • 특징 부분집합 선택(feature subset selection)

    차원의 저주를 해결하기 위한 방법은 이것도 있습니다. 특징 부분집합 선택이란, 특징의 의미가 중복되거나, 관련이 없는 특징들을 제외하는 것입니다. 예를 들어봅시다.

    • 특징의 의미가 중복 : 제품의 구입 가격과 판매 세금 가격
    • 관련이 없는 특징 : 학생들의 성적 데이터를 학습하는 모델에서 학생들의 ID

    그러나 이걸 항상 우리가 일일이 고를 수 없을 지도 모릅니다. 그래서 다음의 방법들로 특징의 부분집합을 선택하는 것 같습니다.

    • 삽입 방법 : 데이터 마이닝 알고리즘 자체에서 사용할 특징과 무시할 특징을 결정 (ex:의사 결정 트리)
    • 필터 방법 : 데이터 마이닝 알고리즘을 실행하기 전에 독립적인 방법으로 특징들을 선택 (ex:상관관계가 낮은 속성들끼리를 선택)
    • 래퍼 방법 : 특징 부분집합의 최고 조합을 찾기 위해 데이터 마이닝 알고리즘을 블랙박스로 사용

    필터/래퍼의 자세한 방법은 책의 60p~61p를 확인합시다.

  • 특징 생성(feature creation)

    원래의 특징들로부터 데이터 집합의 중요 정보를 더 효과적으로 표현하는 새로운 특징 집합을 생성하는 것을 말합니다. 새 특징들의 수는 기존의 특징들의 수보다 적을 수 있어서, 차원 축소가 됩니다! 2가지의 방법이 있습니다.

    • 특징 추출 : 원본 데이터로부터 특징의 새로운 집합을 생성하는 것입니다. 예를 들면, 사람 얼굴이 256x256픽셀 이미지에 있다고 해봅시다. 그럼 이것은 사실 256x256의 특징이 있다고 볼 수 있습니다. 이 픽셀 집합을 사용하는 것보다, 어떤 전처리를 통해서 사람의 눈,코,입 과 같은 어떤 특징들을 추출하면 다양한 종류의 분류 기법들을 적용할 수 있습니다.
    • 데이터의 새로운 공간으로의 매핑 : 데이터를 아예 새로운 관점으로 바꿔서 표현하는 것입니다. 예를 들어봅시다.
    푸리에
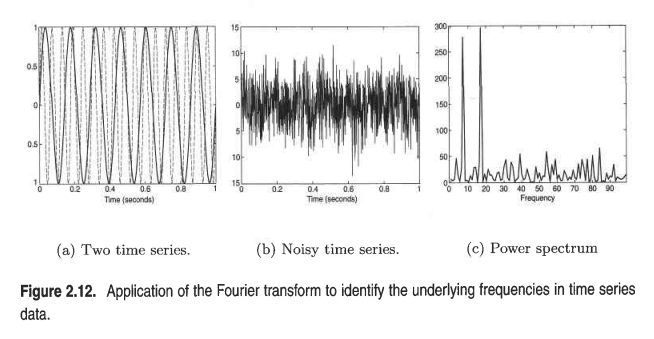
    시계열 데이터 sin함수

    시계열 데이터 sin함수 2개에 noise가 껴있다고 해봅시다(b). 이것은 한눈에 보기엔 무슨 데이터인지 모르지만, 푸리에 변환을 적용해서 frequency 도메인으로 넘어가면 (c)처럼 2개의 sin함수들이 어떤 주파수를 갖는지 확인할 수 있습니다.

  • 이산화와 이진화(discretization and binarization)

    카테고리형 feature들에 정수 0,1,2,..를 매겨서 string feature를 숫자 데이터로 만드는데 의의가 있습니다. 그리고 원-핫 인코딩 혹은 멀티-핫 인코딩처럼 feature를 sparse한 vector로도 만들 수 있습니다.

    • 연속형 속성의 이산화 histogram을 떠올리면 됩니다. 범위를 지정해서 범위내의 데이터들을 하나의 카테고리에 속한다고 표현하는 것이죠. 이때, 핵심 쟁점은 구간 분리를 어떤 방식으로 할 것인지, 분리 지점을 어디로 정할지입니다.
    • 비지도 이산화(unsupervised discretization) 분류를 위한 이산화 방법에는 클래스 정보를 사용(supervised)하는지, 안하는지(unsupervied)의 차이가 있습니다. 클래스 정보를 사용하지 않으면, 다음의 예시들이 있다.
      • equal width method : 그냥 임의로 사용자가 구간을 설정함. 더 나은 방법으론 equal frequency/equal depth가 있다.
      • 7장에서 배울 K-means를 이용한 방법도 있다.
    • 지도 이산화(supervised discretization) 클래스 정보를 이용해서 데이터를 이산화합니다. 2개의 부류가 있네요.
    • 상향식 : 초기 데이터를 하나의 분리 구간들로 시작해서 통계적 시험 결과가 유사한 인접 구간들을 합병해 더 큰 구간을 생성하는 방법
    • 하향식 : 2분할 상태에서 최소 엔트로피를 갖도록 구간을 분리하고, 각각의 구간에서 또 2분할하는 방식으로 진행되는 방법 엔트로피란 다음과 같습니다.
    \[e_i=-\sum_{j=1}^k p_{ij} \log_2 p_{ij}\]

    ※ $p_{ij}$는 i번째 구간에서 클래스 j의 확률이고, k는 클래스 레이블들을 얘기함.

    분할의 전체 엔트로피는 개별 구간의 엔트로피의 weight mean이 됩니다. 한마디로 데이터의 수가 많을 수록 그쪽에 가중치를 더 둔다는 의미입니다.

    \[e=\sum_{i=1}^n w_ie_i\]

    ※ n은 구간의 수, $w_i=m_i/m$으로 i번째 구간의 값들의 비율이고 $m_i$는 i번째 구간의 데이터의수, m은 전체 데이터 수이다.

    직관적으로 각 구간의 분리가 잘돼서 엔트로피가 작아지면 전체 엔트로피도 작아져서 질서정연함을 보는 것입니다.

  • 변수 변환(variable transformation)

    여기부턴 .. 편하게 얘기하겠다.

    feature들을 다른 값으로 변환하는 기능이다.

    • 단순 함수 : 변수가 x면 단순 함수 f(x)를 이용해서 데이터를 변환
    • standardization or normalization : feature들의 scale이 다를 경우, scale이 큰 쪽만 분류의 기준이 될 수 있다. 따라서 각각의 scale들을 평균이 0, 표준 편차가 1인 범위로 바꿔야 한다.



유사도(similarity)와 비유사도(dissimilarity)의 척도

정의

유사도란, 두 객체의 닮은 정도에 대한 수치적인 척도이다. 객체가 비슷할수록 측정 값이 커진다. 비유사도란, 두 객체의 다른 정도에 대한 수치적인 척도이다. 객체가 비슷할수록 측정 값이 작아진다. distance가 자주 동의어로 사용된다. 근접도(proximity)란 용어를 유사도나 비유사도 모두를 지칭하기 위해 본 글에서 사용한다.


변환

유사도와 비유사도 간의 변환과 scale을 [0,1]과 같은 특정 범위로 변환해줄 때 쓴다.

유사도의 scale 변환의 예시는 최소 최대 값을 0과 1로 매핑시켜주는 선형 변환이다.

\[s = \frac{s-s_{min}}{s_{max}-s_{min}}\]

근접도가 [0,$\infty$]처럼 $\infty$가 있는 경우, 비선형 변환이 필요하다. 식은 다음과 같다.

\[d'=\frac{d}{1+d}\]

그러나, 비유사도의 값이 0,0.5,2,10,100,1000이라면 변환된 값은 0.33,0.67,0.9,0.99,0.999로 변환된다. 실제 값은 점점 굉장히 커지는 경향을 갖지만, 변환된 값에선 점점 distance가 압축되는 느낌이 있으므로, 상황에 따라 주의해야한다.

더 다양한 방법들이 책에 나와있다.

단순 feature간의 유사도와 비유사도

명목형 feature(binary 느낌)은 논리 연산자 and 를 생각하면 되고, 카테고리형 feature는 정의할 수 있으나.. 문제가 있다. 예를 들어 데이터 객체가 [soso,good,nice,not bad] 일 경우 soso와 not bad의 거리는 4-1=3이지만, soso와 good의 거리는 1이다. 그럼 soso와 not bad가 더 유사하지 않다는 의미인가? 이것은 문제가 될 수 있으니 주의하자.

데이터 객체간의 비유사도

다양한 종류의 비유사도가 존재한다.

  • minkowski distance : $d(x,y) = (sum_{k=1}^n x_k-y_k ^r)^\frac{1}{r}$
    • r=1 : 두 이진 벡터간의 다른 비트의 수를 얘기하는 해밍 거리(Hamming distance)
    • r=2 : 유클리드 거리($L_2$ norm)
    • r=$\infty$ : 최고 거리($L_{\infty}$ norm). 객체들의 임의의 feature들 간의 최대 거리를 얘기함.

유클리드 거리는 다음의 성질을 만족한다.

  1. 양의 성질
    1. 모든 x와 y에 대해 $d(x,y)>=0$
    2. x=y일 경우, $d(x,y)=0$
  2. 대칭성
    1. 모든 x와 y에 대해 $d(x,y)=d(y,x)$
  3. 삼각 부등성 $d(x,z)<=d(x,y)+d(y,z)$ 이 성질 모두를 만족시키는 척도를 metrics이라고 한다.

  • 데이터 객체간의 유사도

    유사도의 경우, 삼각 부등성은 성립하지 않지만, $s(x,y)$를 x,y간의 유사도라고 할 때, 다음의 양의 성질과 대칭성이 성립한다.

    1. $x=y$일 경우, $s(x,y)=1$
    2. $\forall x,y$, $s(x,y)=s(y,x)$



근접도 척도의 예

근접도 척도의 예시(page 80)부터는 제일 마지막에 정리한다. 책의 주요 기법들부터 정리하자.

7 분 소요

참고