뽀또12

인공지능을 공부하는 사람들하고 많은 지식을 공유하고, 제가 아는 것을 많이 알려드리고 싶습니다.

정말 하고 싶은게 너무 많아요. 모두들 항상 즐겁고 행복하게 열심히 삽시다! 오늘도 파이팅입니다!

업데이트:

카테고리: ,

현재 저는 Mulit class classification을 통해 real time으로 object semantic segmentation을 사용하고, Densefusion으로 real time 6D-POSE를 하는 것을 목표로 하고 있습니다.

혼자서 계속 딥러닝을 공부하고, 여러 네트워크를 파보고 직접 코드를 작성하면서 짧은 기간동안 많은 발전을 한 것 같습니다.. 예를 들면 Class를 작성하는 방법이나 dataset.py를 만드는 방법, loss.py를 만드는 방법, 데이터를 다루는 방법 등 많은 것을 알게 되었네요.

그러나 계속 학습을 진행할때마다 큰 걸림돌이 되는게 있었는데요. 바로 Loss function을 사용하는 것입니다. 특히 Multi class classfication에 매우 효과적인 loss function인 Cross Entropy 함수가 어떻게 작동하는 것인지 몰라서 이번 기회에 정리를 해보려고 합니다.

※ 참고로 classfication의 class 수가 2개일 경우, binary cross entropy 함수를 쓴다고 하네요.

Cross Entropy를 예제를 통해 접해봅시다

예시를 통해 살펴봅시다.

분류하고자 하는 class를 [1, 2, 3]이라고 하자. 그리고 입력 이미지로 999장을 준비할 것인데, Minibatch를 사용한다고 하고, batch size = 3으로 지정한다. 그리고 첫번째 Minibatch인 Minibatch 1st를 예시로 사용하여 minibatch의 Cross Entropy(CE) Loss를 확인해보자.


설명을 위한 준비

batch set의 3장의 이미지의 정답 label이 다음과 같다고 하자.

  • 첫번째 이미지의 정답 label = 1 -> x = 1
  • 두번째 이미지는 정답 label = 2 -> x = 2
  • 세번째 이미지는 정답 label = 3 -> x = 3

그리고 convolution & FC layer 네트워크를 통해, 3개의 output $ ( y_i | y_i \in [ y_1 , y_2 , y_3 ] ,\;i = 1,2,3 )$이 나오도록 학습을 진행할거고 네트워크의 끝단에 Softmax 함수 S를 사용하여 $S(y_i)$를 얻는다.

※ 참고로 pytorch의 nn.CrossEntropyLoss()는 내부에 softmax가 있어서 굳이 네트워크 끝단에 추가할 필요가 없다네요.

$\Sigma P(y_i) = 1$을 만족하며, $P(y_i)$의 뜻은 다음과 같다.

입력 이미지의 object가 네트워크로 인해 예측되는 값 $y_i$는 각 데이터들이 class $x_i$ 에 해당할 확률을 이야기한다.

예를 들어, $P( y_1 )= 0.8 ,\;S( y_2 ) = 0.1,\;S( y_3 )= 0.1$ 이면 입력 이미지 속 object의 확률은 다음과 같다.

  • x=1일 확률은 0.8
  • x=2일 확률은 0.1
  • x=3일 확률은 0.1

즉, object가 80%의 확률로 object label이 1이라는 추론을 할 수 있다.

어쨌든, 이렇게 해서 Cross Entropy를 알기 위한 준비가 끝났다.


본격적인 cross entropy 예제 시작!

Cross Entropy는 다음과 같은 식을 만족한다.

식1

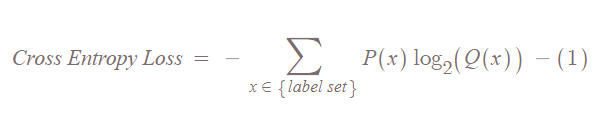
솔직히 이 식만 보면 무슨 이야기를 하는지 감이 팍 안온다. 그래서 위에 softmax 확률을 예시로 들었던 것을 사용해서 그림으로 정리해보았다.

우선 target을 지정한다. 먼저 입력 이미지안의 object의 정답 label이 1이라고 해보자. 이제 아래 계산을 통해 Cross Entropy(CE) Loss가 어떻게 구해는지 확인해 보자.

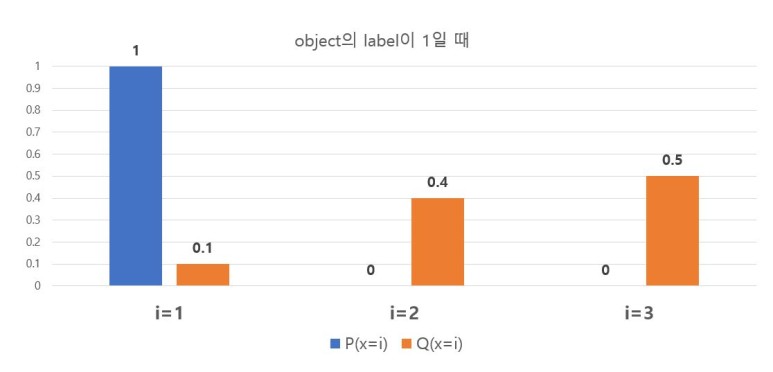
첫번째 이미지 ( label = 1 : x = 1)가 네트워크에 입력되어 클래스일 확률 $S(y_i)$이 출력돼 그림 1로 표현되었다.

그림1
그림 1

※ $Q(x=i) = S(y_i)$이다.

P는 정답 확률, Q는 예측한 확률이다. target label이 1일때, $P(x=1) = 1$일 것이다. 그리고 $P(x=2)=P(x=3) = 0$이다. CEloss 식에 의해서, 그림 1의 경우 Minibatch 1st의 첫번째 이미지가 target label = 1이므로 label = 1인 첫번째 이미지의 $loss_{label = 1} = - P(x=1)log_2(S( y_1 )) = 3.3219$ 이다.

그림2
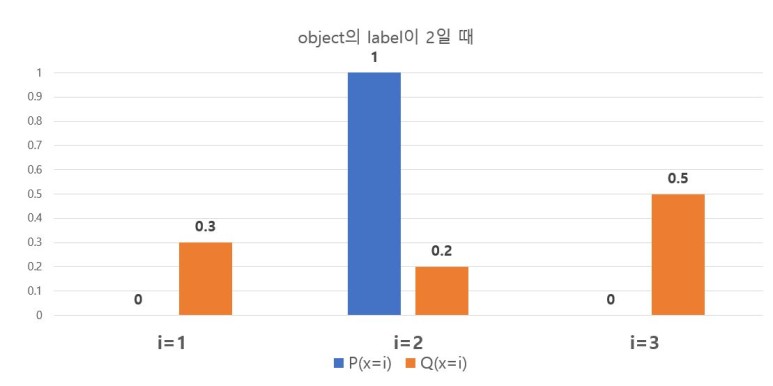
그림 2

그림 2는 Minibatch 1st의 두번째 이미지(target label = 2)의 결과를 표현한 것이다. CEloss 식에 의해서, label = 2인 두번째 이미지의 $loss_{label=2} = - P(x=2)log_2(S( y_2 )) = 2.3219$ 이다.

그림3
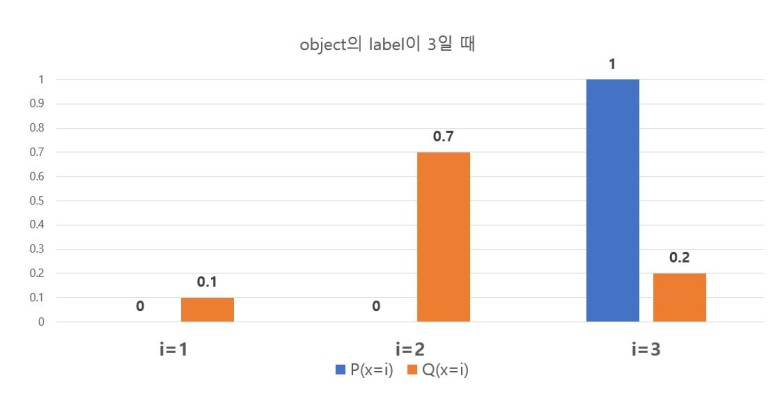
그림 3

마지막으로 그림 3은 Minibatch 1st의 세번째 이미지(target label = 3)의 결과를 표현한 것이다. CEloss 식에 의해서, label = 3인 세번째 이미지의 $loss_{label=3} = - P(x=3)log_2(S( y_3 )) = 2.3219$ 이다.

따라서 식(1)에 의해서 전체 CELoss는 다음과 같다.

\[CEloss = loss_{label=1} + loss_{label=2} + loss_{label=3} = 7.966\]

이제 어느정도 Epoch가 돌아서 (과장해서 100번이 돌아서) 학습이 많이 됬다고 생각하고 101번째의 Minibatch 1st를 다시 봐보자. 1,2,3번째 이미지를 순서대로 보여줄 것이므로, 설명은 생략하고 그림과 loss 값만을 적겠다.

  • Minibatch 1st의 첫번째 이미지

    그림4
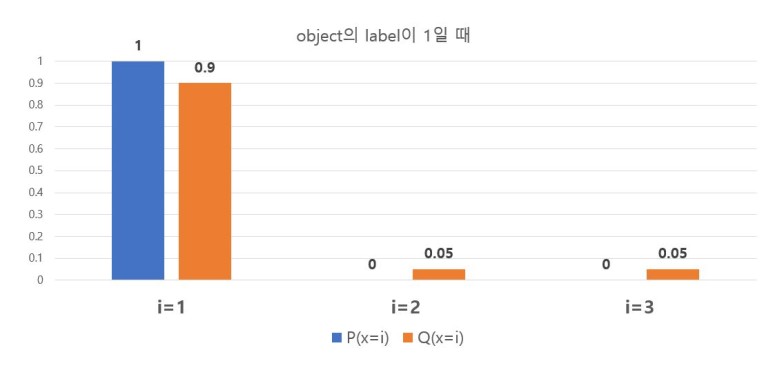
    그림 4
    • $loss_{label=1} = - P(x=1)log_2(S( y_1 )) = 0.1520$

  • Minibatch 1st의 두번째 이미지

    그림5
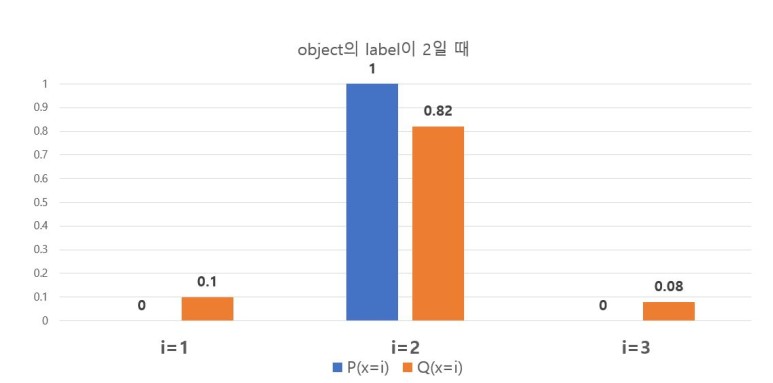
    그림 5
    • $loss_{label=2} = - P(x=2)log_2(S( y_2 )) = 0.2863$

  • Minibatch 1st의 첫번째 이미지

    그림6
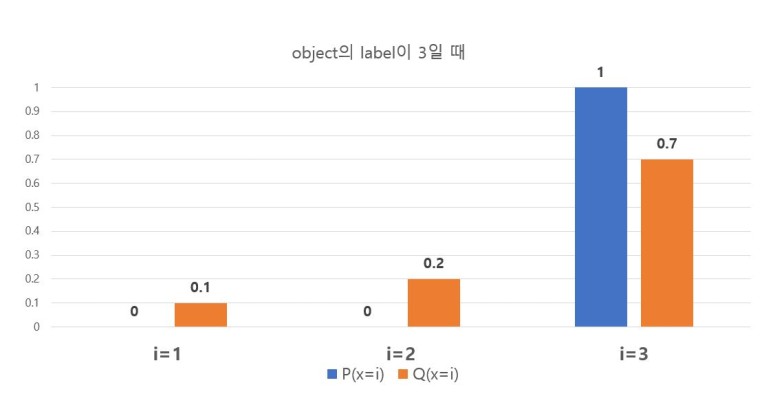
    그림 6
    • $loss_{label=3} = - P(x=3)log_2(S( y_3 )) = 0.5145$

따라서 CEloss식에 의해서 어느정도 학습된 모델의 전체 CELoss는 다음과 같다.

\[CEloss = loss_{label=1} + loss_{label=2} + loss_{label=3} = 0.8008\]

학습이 잘 이뤄진다면, 예측한 $y_i$ 의 softmax 값이 커지게 되고 CEloss가 줄어듦을 볼 수 있다.

3 분 소요

참고