뽀또12

인공지능을 공부하는 사람들하고 많은 지식을 공유하고, 제가 아는 것을 많이 알려드리고 싶습니다.

정말 하고 싶은게 너무 많아요. 모두들 항상 즐겁고 행복하게 열심히 삽시다! 오늘도 파이팅입니다!

업데이트:

카테고리: ,

1. Gradient Descent

경사하강법이라고 불리는 Gradient descent는 Convex loss function을 최소화 하는 weight를 찾기 위해 사용하는 optimizer이다. 반복적으로 기울기가 깊어지는 방향으로 조금씩 움직이는 모습을 상상하면 되는데, 가장 흔한 예시로 loss function을 2차 함수를 생각하면 된다.


1.1 예제

아래의 이미지는 경사 하강법의 예시를 표현한 것이다.

2차함수

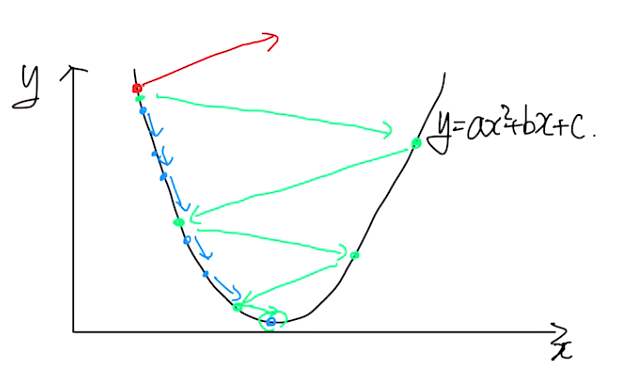
2차 함수 $y=ax^2+bx+c$를 간단히 $y=(x-5)^2+5$라고 해보자. 이것의 목표는 “y가 최소가 되는 지점은?”이다. 그리고 위 이미지를 생각하면서 현재 파란 점의 첫 시작이 $x=3$이라고 하자.

이제 $y=(x-5)^2+5$를 $x=3$에서 미분을 하면, 다음과 같다.

\[\frac{dy}{dx}|_{x=3} = 2(3-5) = -4\]

즉 $x=3$에서의 기울기는 -4가 되고, 이는 파란색 화살표 방향으로 뻗어나갈 수 있게 해주는 동력이 된다. 경사 하강법은 loss function을 최소화하는 weight를 찾는 optimizer라고 했는데 여기선 $x$가 일종의 weight라고 생각하면 된다.

경사 하강법에 의해 $x$를 업데이트 하는 식은 다음과 같다.

\[x_{t+1} = x_{t} - \eta \frac{dy}{dx}|_{x_{t}}\]

위 식을 이용하면 우린 $x=3$일 때를 t=1이라 하면 다음 $x_2$는 다음과 같이 구할 수 있다.

\[x_{2} = 3 + \eta * 4\]

여기서 $\eta$는 학습률(learning rate) 라고 불린다. 이 학습률은 원하는 파라미터를 찾는데 지대한 영향을 미친다. 왜그럴까?? 여기서 $x=3$일 때, $\eta$의 예시에 따라 결과가 어떻게 변할지를 한번 살펴보자.

  1. $\eta=0.1$
  2. $\eta=0.5$
  3. $\eta=0.8$
  4. $\eta=10$

$\eta=0.1$ 일 때

\(x_{2}=-2(3-5)*\textbf{0.1}+3=3.4\) 위 식처럼 계속해서 진행하다보면 위 그림에서 파란색 선처럼 조금씩 최적점으로 수렴하게 될 것이다.

$\eta=0.5$ 일 때

\(x_{2}=-2(3-5)*\textbf{0.5}+3=5\) 이번엔 우연찮게 한번에 loss function을 최소로하는 최적점을 찾아버렸다.

$\eta=0.8$ 일 때

\(x_{2}=-2(3-5)*\textbf{0.8}+3=6.2\)

\[x_{3}=-2(6.2-5)*\textbf{0.8}+6.2=4.28\]

위 식처럼 계속해서 진행하다보면 위 그림에서 초록색 선처럼 넓게 뛰면서 최적점으로 수렴하게 될 것이다.

$\eta=10$ 일 때

\(x_{2}=-2(3-5)*\textbf{10}+3=43\)

위 식처럼 계속해서 진행하다보면 위 그림에서 빨간색 선처럼 멀리 가버릴 것이다.


1.2 결론

결과를 보다시피, 학습률 $\eta$는 학습할 때 있어서 굉장히 간단하면서도 중요한 파라미터 임을 잊지말고, 실험적으로 가장 좋은 학습률을 찾는 것이 현재 내가 알고있는 최선이다. (사실 git에 올라와있는 네트워크를 사용한다면, 주어진 그대로를 사용하는게 가장 좋기도 하다.)

이렇게 우리는 학습률과 미분을 통해서 업데이트하고자 하는 파라미터를 매번 갱신해줄 수 있고, 기울기에 따라 하강 방향을 정하게 되므로 이것을 경사 하강법(gradient descent)이라고 부른다.




2. SGD(Stochastic Gradient Descent)

확률적 경사 하강법(Stochastic Gradient Descent)은 데이터를 학습의 iteration이 돌아갈 때마다 무작위로 섞어서 경사 하강법을 적용시킨 것이라고 한다. 이렇게하면 local minimum에 빠지는 것을 많이 방지해 준다고 한다.


2.1 의문점 및 생각

의문점

근데 내가 공부한 배치 학습에 따르면, 미니 배치 학습 부분에서 이미 전체 데이터에서 데이터를 무작위로 추출해서 batch를 만든다고 했다. 그럼 그냥 미니 배치 학습으로 경사 하강법을 사용하면 그거 자체가 확률적 경사 하강법이 된게 아닐까..? 음.. 명확하게 끊어지질 않는다.. 그래서 인터넷에 찾아보니 확률적 경사 하강법에 대해 소개하는 글에서 다음과 같이 SGD의 예시 코드를 보여준다.

import numpy as np

def sgd(
    gradient, x, y, start, learn_rate=0.1, batch_size=1, n_iter=50,
    tolerance=1e-06, dtype="float64", random_state=None
):
    # Checking if the gradient is callable
    if not callable(gradient):
        raise TypeError("'gradient' must be callable")

    # Setting up the data type for NumPy arrays
    dtype_ = np.dtype(dtype)

    # Converting x and y to NumPy arrays
    x, y = np.array(x, dtype=dtype_), np.array(y, dtype=dtype_)
    n_obs = x.shape[0]
    if n_obs != y.shape[0]:
        raise ValueError("'x' and 'y' lengths do not match")
    xy = np.c_[x.reshape(n_obs, -1), y.reshape(n_obs, 1)]

    # Initializing the random number generator
    seed = None if random_state is None else int(random_state)
    rng = np.random.default_rng(seed=seed)

    # Initializing the values of the variables
    vector = np.array(start, dtype=dtype_)

    # Setting up and checking the learning rate
    learn_rate = np.array(learn_rate, dtype=dtype_)
    if np.any(learn_rate <= 0):
        raise ValueError("'learn_rate' must be greater than zero")

    # Setting up and checking the size of minibatches
    batch_size = int(batch_size)
    if not 0 < batch_size <= n_obs:
        raise ValueError(
            "'batch_size' must be greater than zero and less than "
            "or equal to the number of observations"
        )

    # Setting up and checking the maximal number of iterations
    n_iter = int(n_iter)
    if n_iter <= 0:
        raise ValueError("'n_iter' must be greater than zero")

    # Setting up and checking the tolerance
    tolerance = np.array(tolerance, dtype=dtype_)
    if np.any(tolerance <= 0):
        raise ValueError("'tolerance' must be greater than zero")

    # Performing the gradient descent loop
    for _ in range(n_iter):
        # Shuffle x and y
        rng.shuffle(xy)

        # Performing minibatch moves
        for start in range(0, n_obs, batch_size):
            stop = start + batch_size
            x_batch, y_batch = xy[start:stop, :-1], xy[start:stop, -1:]

            # Recalculating the difference
            grad = np.array(gradient(x_batch, y_batch, vector), dtype_)
            diff = -learn_rate * grad

            # Checking if the absolute difference is small enough
            if np.all(np.abs(diff) <= tolerance):
                break

            # Updating the values of the variables
            vector += diff

    return vector if vector.shape else vector.item()

여기서 iteration 부분을 캐치해보면 다음과 같다

# Performing the gradient descent loop
for _ in range(n_iter):
    # Shuffle x and y
    rng.shuffle(xy)

    # Performing minibatch moves
    for start in range(0, n_obs, batch_size):
        stop = start + batch_size
        x_batch, y_batch = xy[start:stop, :-1], xy[start:stop, -1:]

        # Recalculating the difference
        grad = np.array(gradient(x_batch, y_batch, vector), dtype_)
        diff = -learn_rate * grad

        # Checking if the absolute difference is small enough
        if np.all(np.abs(diff) <= tolerance):
            break

        # Updating the values of the variables
        vector += diff

위 코드를 해석해보면 작동 방식은 다음과 같다.

  1. Epoch만큼의 iteration이 시작할 때, 먼저 전체 데이터를 무작위로 섞는다.
  2. 미니 배치 학습을 할 것이므로, 미니 배치로 얻어진 배치의 수만큼 iteration을 돌린다.
  3. gradient를 구하고 업데이트 식을 통해 파라미터들을 업데이트한다.

나의 생각

음.. 그냥 데이터를 무작위로 섞고 미니 배치를 하는 것이 몇년 전까지만 하더라도 local minimum에 빠지지 않으며 네트워크 자체의 안정성 또한 취할 수 있는 가장 좋은 학습 수단이었을 것 같다. 그리고 이 때 경사 하강법을 사용했으면, 그것 자체가 확률적 경사 하강법(Stochastic gradient method)이 되는 것 같다.

4 분 소요

참고