다중 퍼셉트론을 쓰는 이유

다중 퍼셉트론을 쓰는 이유에 대해

밑바닥부터 시작하는 딥러닝 을 읽으면서 다중 퍼셉트론이 왜 나왔는지에 대해 깔끔히 정리가 되어, 기록하고자 본 글을 작성한다.

1.1 퍼셉트론

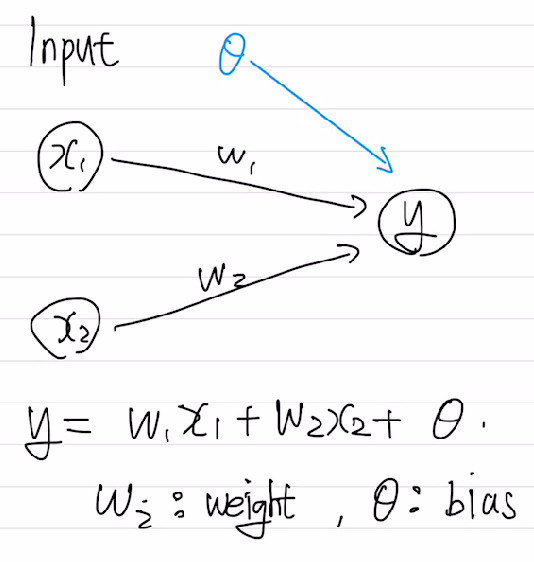
퍼셉트론은 이제 딥러닝을 공부하는 많은 사람들이 알고 있는 개념일 것이다. 입력이 2개인 간단한 퍼셉트론은 다음과 같다.

입력이 들어오면($x_1, x_2$), 가중치들과 결합하고 bias를 더해 새로운 출력($w_1 x_1 + w_2 x_2 + \theta$)을 낸다. 이 때, y는 $w_1 x_1 + w_2 x_2 + \theta$의 값이 0보다 크면 무조건 1을 출력하고, 작거나 같으면 0을 출력한다. 여기서 0과 1은 해당 퍼셉트론(뉴런)을 활성화 시키지 않는다/시킨다를 보여준다고 생각하자.

\(y = \begin{cases} 1\quad {if} \quad w_1 x_1 + w_2 x_2 + \theta\;>\;0 \\ 0\quad {if} \quad w_1 x_1 + w_2 x_2 + \theta\;\leq\;0 \end{cases}\)

1.2 다양한 논리 게이트들

왜 다중 퍼셉트론이 나온지에 대해 알기 위해선, 먼저 논리 게이트들에 대해 알아야한다. 가장 기본적인 다중 퍼셉트론의 예시인 XOR 게이트에 대해 알기 위해 먼저 AND,OR,NAND 게이트에 대해 알아보자. 아래의 논리 게이트들은 단일 퍼셉트론에서 파라미터들을 바꿈으로써 구현할 수 있다.

1.2.1 AND 게이트

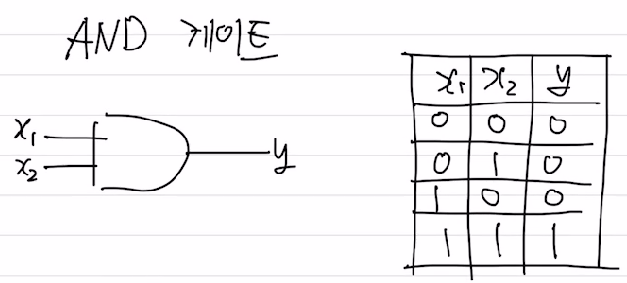
AND 게이트는 “둘 다”여야 한다는 조건이 있다. 게이트의 기호 및 작동 논리는 다음과 같다.

입력에 따른 출력을 얻기 위해 아래 식을 만족하는 $w_1,w_2,\theta$의 조합은 무수히 많다. \(y = \begin{cases} 1\quad {if} \quad w_1 x_1 + w_2 x_2 + \theta\;>\;0 \\ 0\quad {if} \quad w_1 x_1 + w_2 x_2 + \theta\;\leq\;0 \end{cases}\)

많은 조합들 중 하나를 선택하면 된다.

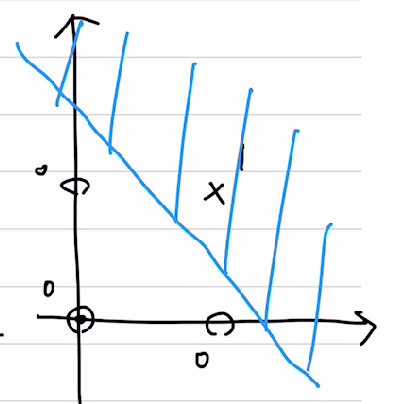
위 조건에 의해 다음과 같은 예시의 범위를 얻을 수 있다.

1.2.2 NAND 게이트

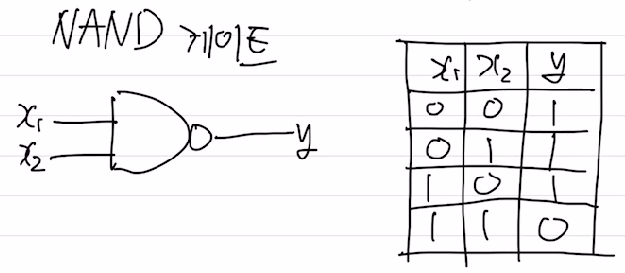
NAND 게이트는 AND 게이트의 끝단에 NOT을 붙인 것이다. 게이트의 기호 및 작동 논리는 다음과 같다.

NAND도 마찬가지로 표를 만족하는 파라미터들을 선택해주면 된다.

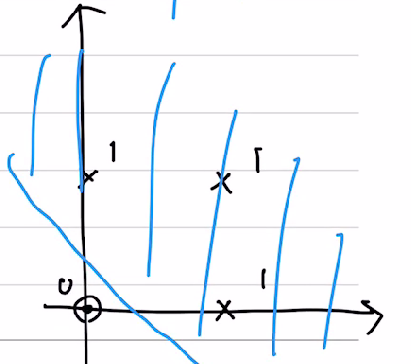
위 조건에 의해 다음과 같은 예시의 범위를 얻을 수 있다.

1.2.3 OR 게이트

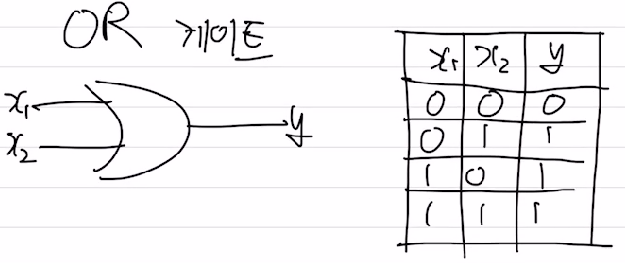
OR 게이트는 “둘 중 하나만이라도”라는 조건이 있다. 게이트의 기호 및 작동 논리는 다음과 같다.

OR도 마찬가지로 표를 만족하는 파라미터들을 선택해주면 된다.

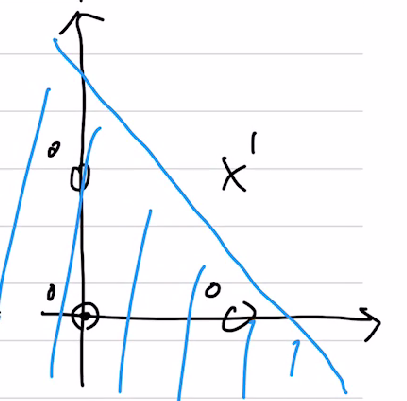
위 조건에 의해 다음과 같은 예시의 범위를 얻을 수 있다.

1.3 XOR 게이트와 다중 퍼셉트론의 관계

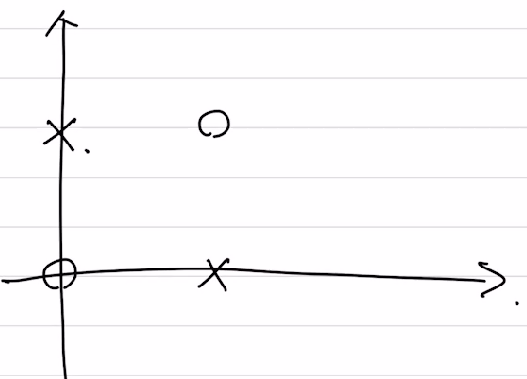
그럼 아래의 분류 문제를 AND,OR,NAND 게이트들처럼 하나의 선을 이용해서 분류할 수 있을까?

절대로 불가능 할 것이다. 즉, 단일 퍼셉트론으론 해결할 수 없게 된다. 따라서 우리는 새로운 게이트를 만들어 내서 해결을 해야하는데, 그 해결책은 바로 XOR 게이트라는 것이다.

1.3.1 XOR 게이트

XOR 게이트는 “둘 중 하나만” 이라는 조건이 있다. 게이트의 기호 및 작동 논리는 다음과 같다.

1.3.2 다중 퍼셉트론

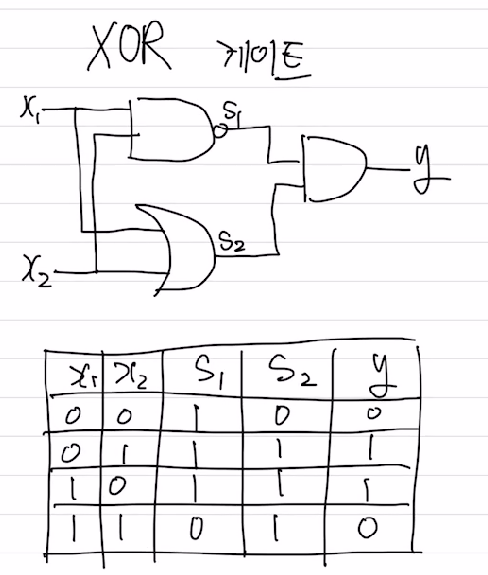
우린 XOR 게이트를 위에서 알게된 논리 게이트들을 섞어서 만들 수 있으며, 위 그림에서의 분류 문제를 간단히 해결할 수 있게 된다.

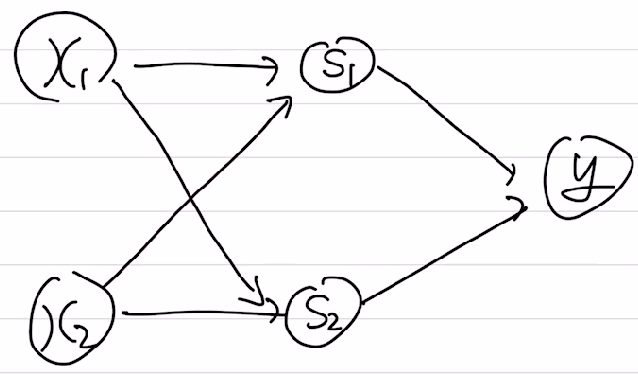
여기서 주목해야할 점은 기존의 입력 $x_1,x_2$가 바로 출력 y에 관여하지 않고 중간에 $s_1,s_2$를 만들어낸다는 것이다. 즉, 입력 층 -> 중간 층 -> 출력 층 의 구조를 가지게 되는데, 이를 퍼셉트론처럼 그래프로 그리면 다음과 같다.

이는 총 3개의 단일 퍼셉트론들로 구성됨을 볼 수 있다. 단일 퍼셉트론들이 모여 다중 퍼셉트론이 되서 층이 생겼으며, 그 결과로 더 복잡한 분류 문제를 풀어낼 수 있게 된다. 이것은 딥러닝의 가장 근원이 되는 개념이다. 퍼셉트론이 많아질수록, 층이 깊어질수록 우리는 새로운 문제들에 도전할 수 있다.

1.3.3 문제점 및 나아갈 방향

그런데 여기서 한가지 주의할 점이 있는데, 단일 게이트들은 전부 파라미터들을 갖는 것을 기억해야한다. 가중치와 편향들은 다중 퍼셉트론의 되면 하나의 XOR 게이트에 3개의 단일 게이트 즉, 3개의 단일 퍼셉트론들이 존재하기에, 우리는 3X3의 9개의 파라미터들을 다루게 된다. 지금이야 이걸 그냥 아무 값이나 가중치와 편향에 넣을 수 있지만, 더 많은 퍼셉트론들이 존재하게되면 수작업이 가능할까? 딥러닝은 다행히도 이 문제를 앞으로 배울 back-propagation, gradient descent 과정에서 스스로 학습하는 과정을 보여줄 것이다.

이제 우린 다중 퍼셉트론이 왜 쓰이는지에 대해 간략하게 배우게 되었다.