Vector space & Subspace
업데이트:
카테고리: 선형대수
Vector space
정의
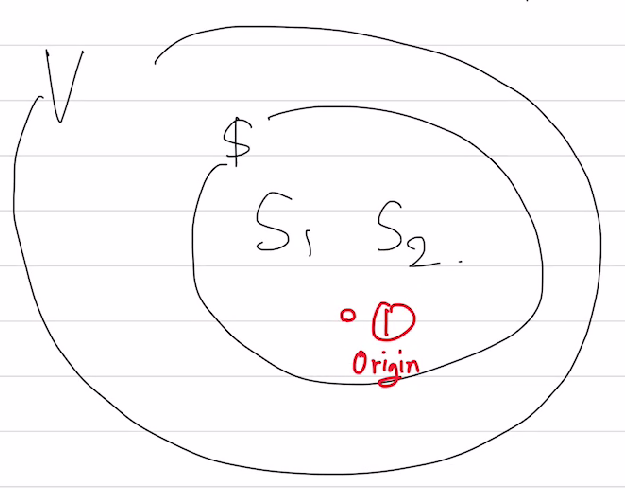
어떤 집합 $V$이 Vector space를 만족하려면, 다음과 같은 두가지 성질을 만족해야한다.(두 성질에 닫혀 있어야한다.(closed))
- for any vetors $x,y \; \in R^n$,
$x,y\; \in V$ -> $x+y \; \in V$ - for any scalar $c\;in R $,
$cx,cy\; \in V$
두 조건을 합치면 다음과 같이 하나로 만들 수 있다.
\[c_1x+c_2y \; \in\; V\;\; (\forall x,y\;\in\;V,\;\forall c_1,c_2\;\in\;R)\]위 조건을 만족해야 우리는 해당 집합 $V$를 Vector space라고 부를 수 있다.
Vector space는 항상 origin을 갖고 있는 것도 잊지 말자.
Subspace
정의
전체 Vector space $V$의 subset $S$가 여전히 Vector space의 조건을 만족한다면, 이것을 Subspace라고 부른다. 즉, $s_1,s_2$가 $S$의 원소일 때, $c_1s_1+c_2s_2 \; \in\; S\;\; (\forall s_1,s_2\;\in\;S\subset V,\;\forall c_1,c_2\;\in\;R)$ 를 만족하면 되는 것이다.
항상 Origin은 모든 Vector space에 속하며 동시에 모든 Subspace에 속함을 잊지말자.