논문 공부: MobileNets: Efficient Convolutional Neural Networks for Mobile Vision Applications - MobileNet V1

본 글은 논문 MobileNet V1을 읽고 공부하는 글입니다.

---

0. Abstract

---

모바일넷은 간결한 구조를 기반으로 하기위해 depthwise separable convolution을 사용해 light weight deep neural network를 만들었다. 저자들은 latency와 accuracy사이의 trade off를 효과적이게 하는 2개의 간단한 global hyperparameter를 소개한다. 이 파라미터들은 model builder가 problem의 제약들에 기반한 자신의 애플리케이션에 적합한 크기의 모델을 선택할 수 있게 해준다.

1. Introduction

---

시간이 흐르면서 높은 정확도를 갖는 복잡하고 deep한 네트워크들이 많이 나왔고 트렌드였다. 그러나 이런 정확도를 향상시키는 네트워크들은 size나 speed에 관해 좀 더 효과적으로 발전시키지 못하였다. 로보틱스, 자율주행차, 증강현실 등 recognition task들은 계산력이 제한된 platform에서 제때 실행되어야 한다. 즉, 네트워크 구조들은 효과적이게 작고 좋은 성능을 보여야한다.

Section 2는 작은 model을 만들기 위한 사전 작업들에 대해 이야기할 것이고, Section 3는 본 네트워크의 구조와 2개의 하이퍼 파라미터들 width multiplier 와 resolution multiplier를 이야기 할 것이다. 이 파라미터들은 네트워크를 보다 더 작고 효율적이게 만든다. Section 4는 실험 결과들에 대해 이야기할 것이고 Section 5는 요약 및 결론을 이야기할 것이다.

2. Prior work

---

이런 효율적인 네트워크를 만들기 위한 많은 접근들은 pretrained network를 압축하거나, 작은 네트워크를 직접적으로 학습시키는 것으로 카테고리화 되었다. 이 논문은 model developer가 그들의 어플리케이션에 대한 (latency, size와 같은) resource restriction들을 충족시키기 위한 작은 네트워크를 특별히 선택할 수 있도록 하는 네트워크 아키텍처의 종류를 제안한다. 모바일넷은 걸리는 시간(latency)를 최적화 하는데 초점을 맞추지만, 작은 네트워크들 또한 만들어낸다. 많은 논문들이 size만 신경쓰지 속도에 대해선 신경쓰지 않는 점과 다르다.

모바일넷은 [26]번 논문에서 처음으로 소개된 depthwise separable convolution으로 부터 주로 만들어지고, 그 다음에, 첫번째의 적은 수의 레이어들에서 계산량을 줄이기 위해 [13]번 논문의 Inception model이 사용 됬다. Flattend networks[16]은 convolution들을 분해한 네트워크를 만들고, 분해된 네트워크들의 잠재력을 보여줬다. 현재 이 논문과 독립적으로, Factorized Networks[34]는 topological connection들의 사용 뿐 아니라, 유사한 factorized convolution을 소개한다. 다음으로, Xception network [3]은 depthwise separable filter들이 inception V3 networks를 능가하기 위해 확장되는지 증명했다. 다른 small network는 Squeezenet [12]이고 이는 아주 작은 small network를 디자인하기위해 bottleneck을 사용한다. 다른 계산량을 줄이는 네트워크들은 structured transform networks [28], deep fried convnets [37]이 예시이다.

small networks를 얻기 위한 다른 접근은 pretrained network들을 압축하거나 분해하거나 줄이는 방식으로 진행했다. literature에서 Compression based on product quantization [36], hashing [2], and pruning, vector quantization and Huffman coding [5] have been proposed . 추가적으로 다양한 factorization들은 pretrained networks [14,20]의 속도를 높이기 위해 제안됬다. small networks를 training하기 위한 방법은 distillation [9]이고 이는 smaller network를 교육하기 위한 larger netowkr를 사용하는 것이다.

3. MobileNet Architecture

---

이제 MobileNet이 만들어지는 핵심 레이어들 (depthwise separable filter)에 대해 이야기할 것이다.

3.1. Depthwise Separable Convolution

depth wise separable convolution은 standard convolution을 depthwise convolution과 pointwise convolution이라 불리는 1X1 convolution으로 분해하는 것을 이야기한다. depthwise convolution은 각각의 입력 채널에 single filter를 적용한다. 그런 다음에 pointwise convolution은 1X1 convolution을 사용해 outputs의 depthwise convolution을 결합한다. 기존의 convolution은 필터와 입력값을 결합해 새로운 output set을 내놓는다. depthwise separable convolution은 이 과정을 2개의 layer들로 쪼갠다. 하나는 filtering을 위한 separate layer 이고, 다른 하나는 combining을 위한 separate layer이다. 이 factorization은 엄청나게 모델의 크기와 계산량을 줄일 수 있다.

그림 1

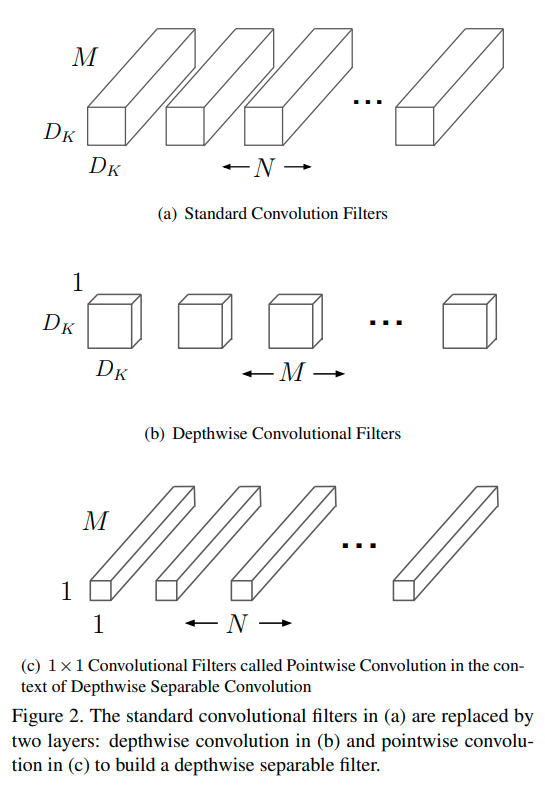
Figure 2.(a)는 standard convolution의 filter를 나타내는데, 이 것은 앞서 말한 것과 같이 2.(b) depthwise convolution, 2.(c) 1X1 pointwise convolution 으로 나뉜다. 기존의 convolutional layer는 입력으로써 \(D_F \times D_F \times M\) 크기를 갖는 feature map F를 갖고 \(D_F \times D_F \times N\) 크기의 feature map G를 만든다. \(D_F\) 는 입력 feature map가 정사각형이라 할 때, width=height를 나타낸다. 다음과 같은 가정을 해보자.

• 입력 이미지의 크기 : $3\times64\times64 = channel\times width\times height
• kernel 정보 :
  • size : $3\times3$
  • 채널의 수 : 100
  • stride = 1
  • padding size = 0

위 계산에 의해서 output의 크기는 width = height = 64가 된다. kernel의 size는 $1\times1$이고 channel이 100이면, 입력과 kernel이 어떻게 연산되고 아웃풋의 채널의 수는 어떻게 될까??

이런 식으로 생각하면 된다.

convolution 연산시 입력 이미지가 (3,64,64)=(채널,width,height) 라면, kernel (3,1,1)=(채널,width,height)가 100개가 있다고 생각하면 된다. 그럼 각각의 kernel들이 입력 이미지와 convolution하여 하나의 output 채널을 형성하게 되고 이렇게 100개가 쌓여서 (100,64,64)가 되는 것이다. convolution 연산을 써보면 다음과 같다.

\[Input\;image(3\times64\times64)\;(*)\;kernel(3\times100\times1\times1) = Output\;image(100\times64\times64)\]

※ (*)는 convolution을 뜻한다 ※ 일반적으로 input image를 input feature map이라고도 부르고 output을 output feature map이라고도 부른다.

이런 방식을 통해서 논문을 생각해봅시다. input feature map (M, DF, DF)=(input의 채널,width of input,height of input)가 들어왔고, kernel(=filter) (M,N,1,1)=(input의 채널의 수 ,kernel의 개수,width of kernel,height of kernel) 으로 convolution을 할꺼다. 그렇게 되면 Output feature map은 (N, DG, DG)=(output의 채널,width of output,height of output) 이 된다. 라는 뜻이다.

기존의 convolution들을 사용했을 때, 계산 비용(computational cost)은 다음과 같이 정의된다.

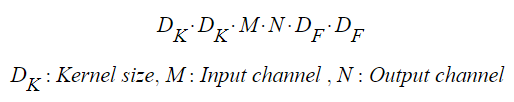
Mobilenet은 이런 term들과 interaction들을 설명한다.

먼저 MobileNet은 $D_k$와 N의 곱셈을 끊기 위해 depthwise separable convolution를 사용한다. 기존의 convolution 연산은 convolutional kernel들에 기반한 feature들을 필터링하고 새로운 표현을 만들기 위해 feature들을 엮는 효과를 가진다. 필터링하고 결합하는 단계들은 depthwise separable convolution을 이용해서 위에서 언급한 computational cost를 상당히 줄여준다!

Depthwise separable convolution(DSC)는 2개의 layer들로 구성되어 있다.

1. depthwise convolutions
2. pointwise convolutions

각 input channel 당 single filter를 적용하기 위해 depthwise convolution을 사용한다. Pointwise convolution은 $1 \times 1$ convolution이다. 이것은 depthwise layer의 output의 linear combination을 만들기 위해 쓰인다. 그리고 MobileNet은 batchnorm과 ReLU를 두 convolution에 이용한다. Depthwise convolution은 input channel당 1개의 filter를 쓰는데, 그 식은 아래와 같이 쓸 수 있다.

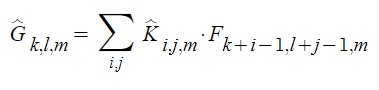
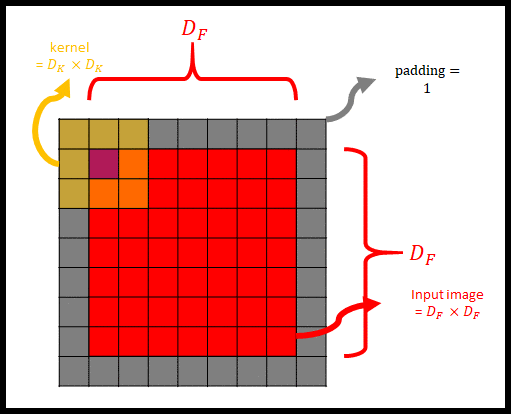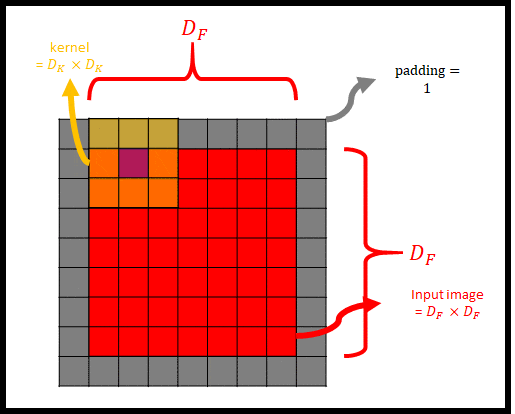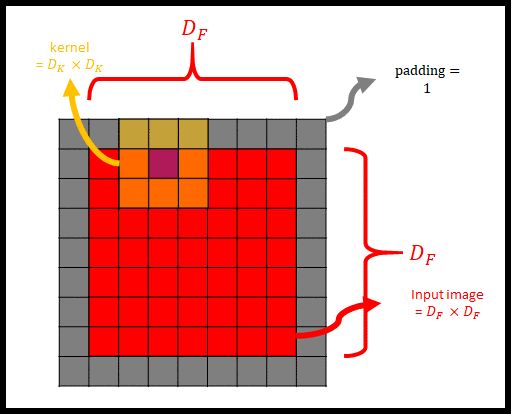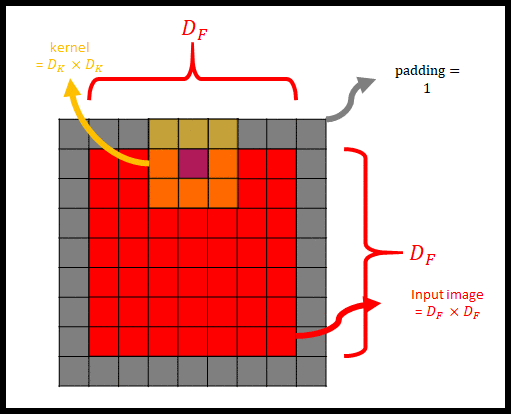
위 수식은 input에 kernel을 취한 것이 output feature map이 된다는 것을 식으로 표현한 것이다. 그림으로 나타내면 다음과 같다.

그림 2

그림 2는 Input image(=input feature map)에 padding을 씌우고 kernel(=filter)를 사용해 convolution을 하는 모습을 나타낸 것이다. 그림 2에서 kernel의 중심과 input image가 겹치는 부분을 보라색 칸으로 표현했다. 여기서 stride = 1이라면, 보라색 칸이 input image를 모두 훑으면서 convolution이 진행될 것이다. 그렇게 되면 kernel이 $D_F \times D_F$ 번 Input image와 padding을 훑으면서 연산이 될 것이다.

그림 2는 channel이 1인 input image의 convolution 과정을 표현했다. 아래 그림 3은 M개의 채널을 가진 input image에 대한 depthwise convolution을 나타낸다.

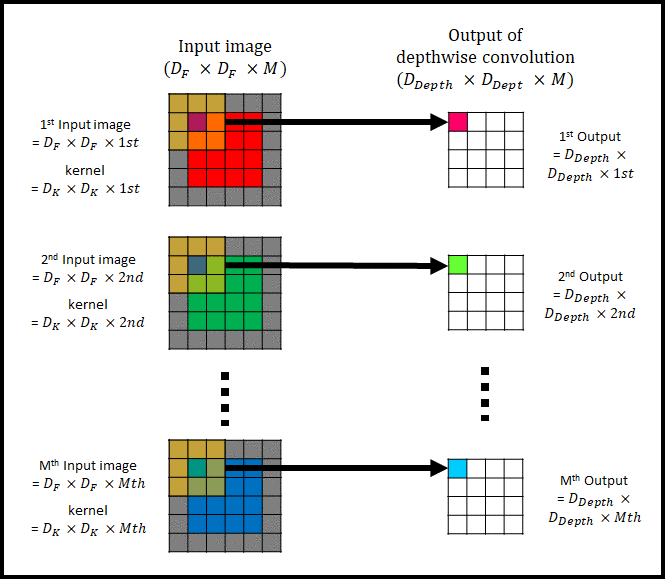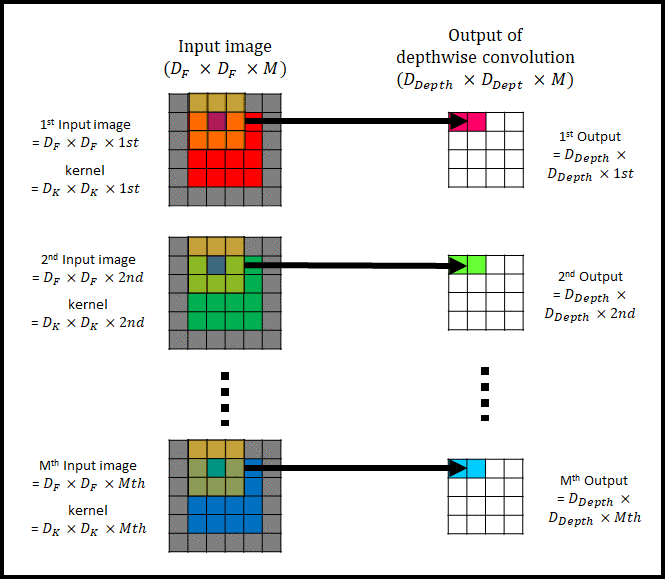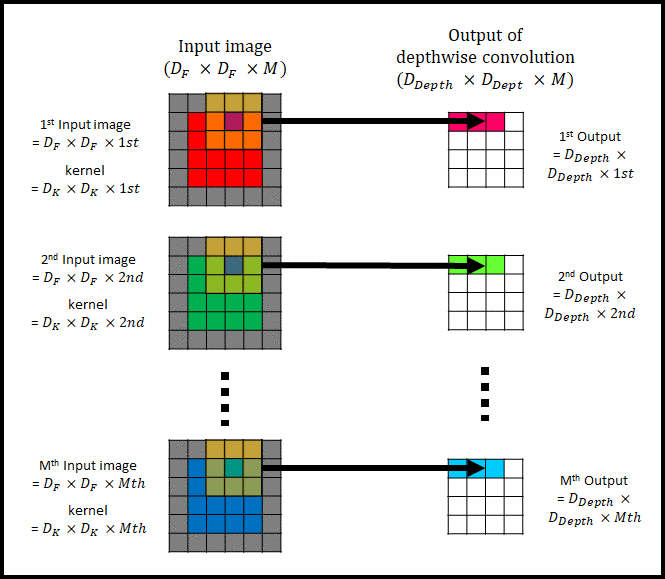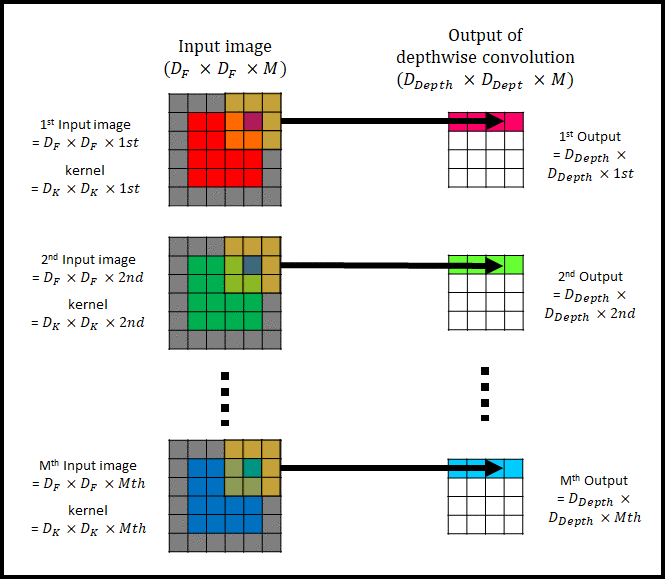그림 3

그림 3은 그림 2를 여러개 사용하여 depthwise convolution을 하는 모습이다. 그림 2를 사용한다고 해서 기존의 convolution과 다른 연산을 하는 것은 아니다. 단지 input image(= Input feature map)의 각각의 channel$( D_F \times D_F \times i_{th} )$에 single filter $(D_K \times D_K \times i_{th} , ⅰ= 1,2, … , N)$를 convolution해서 Output of depthwise convolution $( D_{Depth} \times D_{Depth} \times M )$을 생성하는 것 뿐이다.

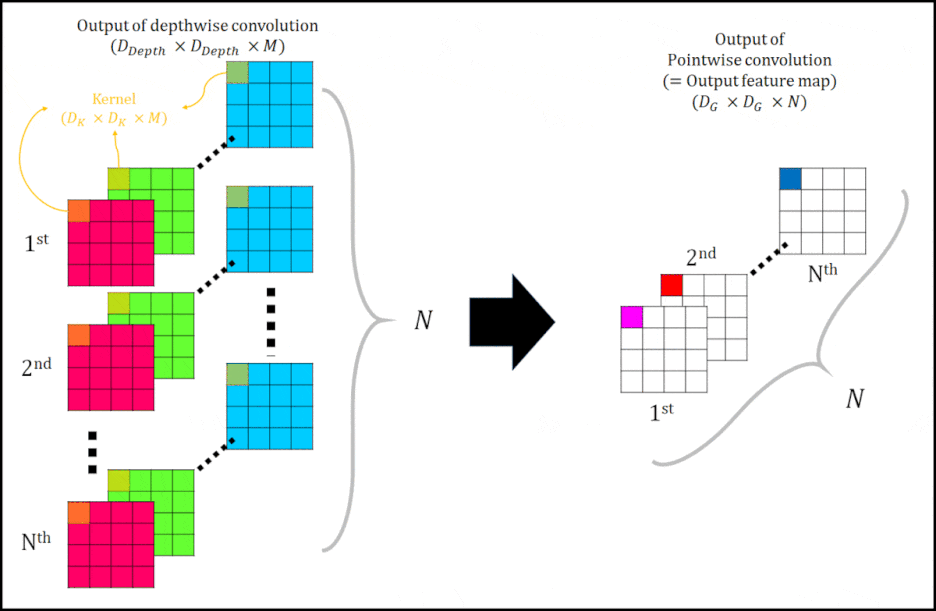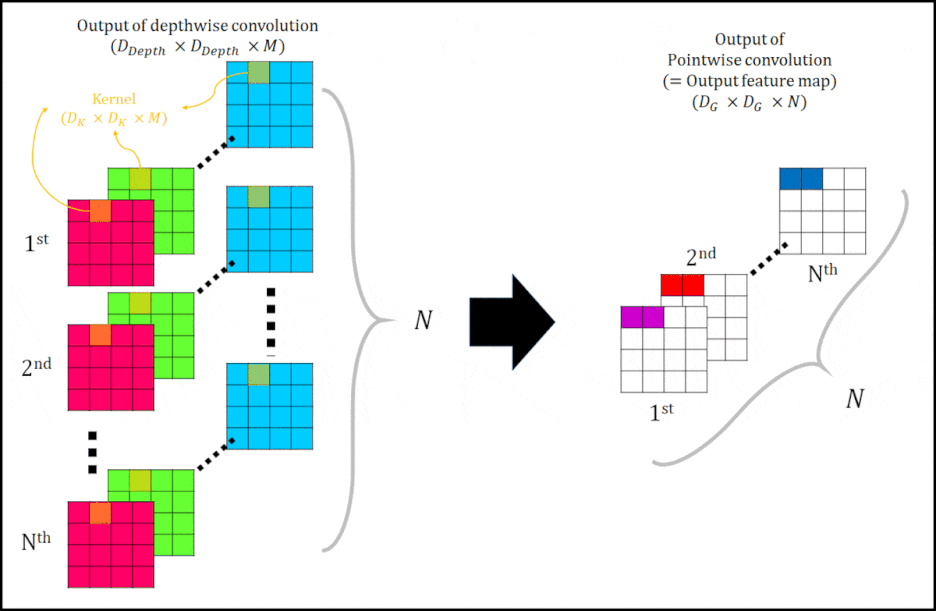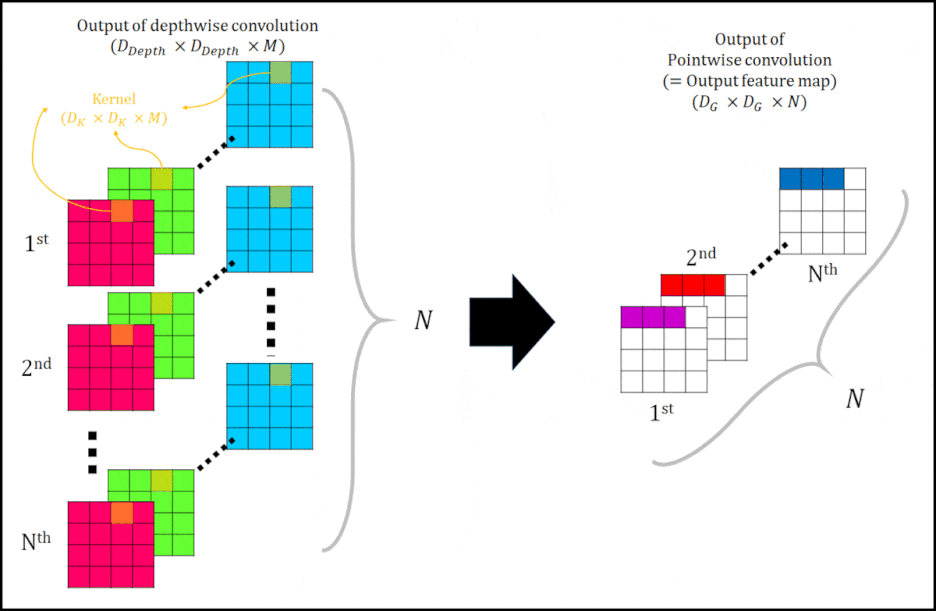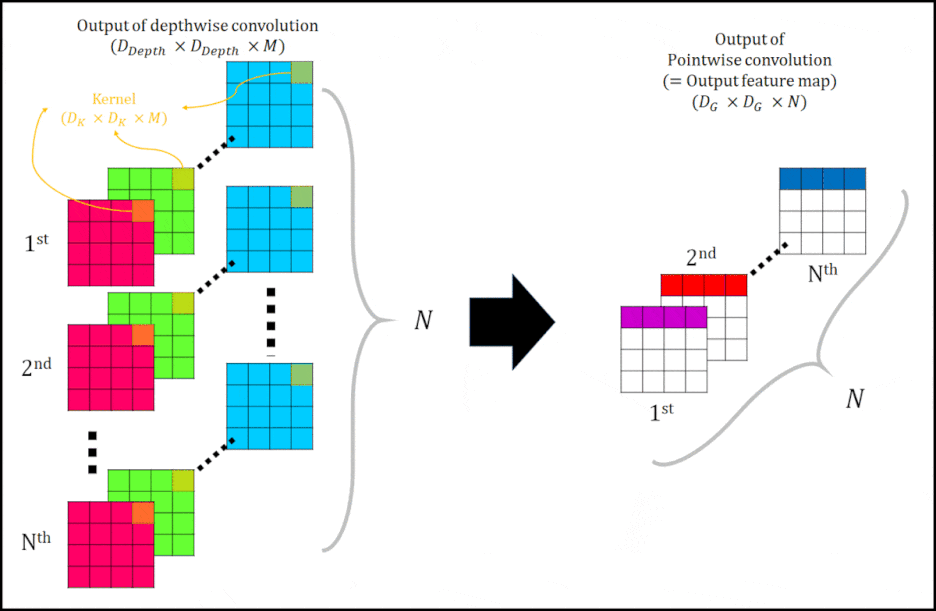
다음으로 Pointwise conovolution에 대해 설명하겠다. 아래 그림 4을 보자.

그림 4 여기서 화살표 좌측에 $N_{th}$와 N은 $M_{th}$와 M으로 정정해야합니다. 잘못 적었네요.

그림 4는 Pointwise convolution 과정을 나타낸다. Output of depthwise convolution $( D_{Depth} \times D_{Depth} X M )$ 을 Kernel $( 1 \times 1 \times M \times N )$ 를 사용하여 convolution을 진행한다. 그렇게 되면 하나의 Pointwise filter에 의해, $1\times 1\times N$의 결과물이 생성됩니다. 다시 말하자면, Output of depthwise convolution을 ⅰ번째 Kernel $( 1 \times 1 \times M )$ 을 사용해 (ⅰ= 1, 2, … , N ) convolution 하는 것을 1st 부터 Nth 까지 반복해 N channel을 갖는 Output image(=Output feature map)$(D_G \times D_G \times N)$을 생성한다.

그러면 이런 과정을 굳이 거치는 이유가 무엇일까?? 그 답은 연산량에 있다.

아래의 모든 과정을 위해 미리 다음과 같은 파라미터들을 가정한다.

• $D_K$ = 3
• padding = 1
• stride = 1

기존의 Input image $( D_F \times D_F \times M )$을 Kernel $(D_K \times D_K \times M \times N)$으로 convolution 한다고 하자.

$D_K \times D_K \times M $ 의 크기를 갖는 Kernel은 $D_F \times D_F$ 번 연산을 하게 되고, $D_K \times D_K \times M$ 의 크기를 갖는 Kernel은 N개 가지고 있으므로 이런 과정을 총 N번 진행하므로 $(D_K \times D_K \times M) \times (D_F \times D_F) \times N$의 연산량을 가진다. 이것은 논문에서 (2)번 식을 의미하고 위에 한번 그림으로 언급한 적이 있다.

하지만 Depthwise separable convolution을 사용하면 연산량이 어떻게 변할까?

먼저 Depthwise convolution을 진행하게 되면, 기존의 Input image $( D_F \times D_F \times M )$의 각 channel을 Kernel $(D_K \times D_K \times 1)$ 으로 연산을 하게되면, Kernel $(D_K \times D_K \times 1)$이 $D_F \times D_F$ 번 연산을 하는데, Input image가 M개의 Channel을 가지므로, Depthwise convolution은 $D_K \times D_K \times D_F \times D_F \times M$ 의 연산량을 가진다.

다음으로 Pointwise convolution을 진행하게 되면, Output of depthwise convolution $( D_{Depth} \times D_{Depth} \times M )$ 을 Kernel $( 1 \times 1 \times M \times N )$ 를 사용하여 convolution을 진행하면, Kernel $( 1 \times 1 \times M )$이 Output of depthwise convolution $( D_{Depth} \times D_{Depth} \times M )$ 과의 convolution 연산을 총 N ( kernel의 개수 ) 개 진행하게 되므로 Pointwise convolution은 $D_{Depth} \times D_{Depth} \times M \times N$ 의 연산량을 가진다.

이제 기존의 convolution 연산량과 Depthwise separable convolution의 연산량을 비교해보자. 기존의 연산량은 $(D_K \times D_K \times M) \times (D_F \times D_F) \times N$ 이다. 저자들이 제안하는 Depthwise separable convolution의 연산량은 $D_K \times D_K \times D_F \times D_F \times M + D_{Depth} \times D_{Depth} \times M \times N$ 이다. 이 때, depthwise convolution을 $D_K$ = 3, padding = 1 , stride = 1 으로 설정하고 진행하면 $D_{Depth}$ 는 $D_F$ 와 같다. 따라서 식을 정리해보면 다음과 같다.

\[\begin{align} & D_K \times D_K \times D_F \times D_F \times M + D_{Depth} \times D_{Depth} \times M \times N \\ &= D_K \times D_K \times D_F \times D_F \times M + D_F \times D_F \times M \times N \\ &= D_F \times D_F \times M \times ( D_K \times D_K + N ) \end{align}\]

Depthwise seperable convolution의 원래 목표가 $D_K$와 N을 분리하는 것이었는데, 이것이 이뤄진 것을 볼 수 있다. 그러나 이게 얼마나 연산량이 줄은건지 감이 오지 않을 수 있다. 그러면 한번 값을 대입해보자. 가정은 다음과 같다.

• $D_K$ = 3
• $D_F$ = 128
• M = 64, N = 128

기존의 convolution 연산량 식에 대입해보면, $3\times 3\times 64\times 128\times 128\times 128\;=\;1,207,959,552$으로 약 12억이다.

Depthwise separable convolution의 연산량을 계산해보면, $128\times 128\times 64\times (3\times 3+128)\;=\;143,654,912$으로 약 1억 4천이다. 약 10분의 1이 줄어든 셈이다! 10분의 1이 얼마 안되는거 같지만, 12억에서 1억4천으로 연산량이 줄었다는 것만 보면 엄청난 계산량의 감소를 직관적으로 알 수 있다.

3.2. Network Structure and Training

MobileNet의 구조는 첫번째 layer에서 full convolution을 쓴 것을 제외하곤 앞서 제시한 Depthwise separable convolution을 사용했다. 기본 구조는 다음 테이블과 같다.

테이블 1) s1, s2는 stride =1 , =2 을 이야기하는데, stride 2를 쓴 경우는 Downsampling을 하기 위해서 사용했다고 한다. dw는 depthwise convolution을 의미한다.

Mult-Adds (Number of Multiply - adds)의 작은 수의 관점에서 네트워크를 간단히 정의하는 것만으론 충분하지 않다. multiply, add같은 연산들을 효율적으로 이용할 수 있게 확실히 하는 것은 중요하다. 저자들의 모델 structure는 거의 dense 1 X 1 convolution에 모든 연산량을 쓰고 있다. 이는 최적화된 general matrix multiply (GEMM) functions으로 이행된다. 대게 convolution들은 GEMM에 의해 이행되지만, im2col이라 불리는 메모리를 GEMM으로 매핑하기 위해 initial reordering을 필요로 한다. MobileNet은 Network의 계산 시간의 95%를 1 X 1 convolution에 소비한다. 또한 Table 2에 보이는 것과 같이 75%의 parabeter들을 가진다. 나머지 25%의 대부분은 Fully Connected에 있다.

테이블 2

모바일넷은 RMSprop을 사용한 TensorFlow에서 학습된다. {파이토치에서 내가 직접 해봤는데, 파이토치에선 원하는 연산을 만들 수 없더라.. 텐서플로에선 가능하다고 글을 보았다} 중요한 점이 두가지가 있다.

1. 크기가 큰 기존의 model들을 학습시키는 것에 반해, MobileNet 같은 작은 네트워크들은 상대적으로 overfiting 문제가 적기 때문에, regularization이나, data augmentation같은 기술들을 조금만 사용했다. 그리고 MobileNet을 학습시킬 때, 저자들은 side heads or label smoothing을 사용하지 않았고, 추가적으로 crop의 사이즈를 작게 제한함으로써 많은 양의 이미지의 왜곡을 줄였다..?
2. 아주 작은 정도거나, no weight decay를 depthwise filter에 사용하는 것. 이 것이 왜 중요하는가? 그 이유는 모델이 작으니까 parameter의 수가 작게 되고 따라서 이런 기능이 거의 필요가 없어졌다는 것이다.

3.3. Width Multiplier : Thinner Models

MobileNet 구조가 이미 작고 낮은 지연시간을 가지지만, 어떤 특정한 경우나 application은 모델을 좀 더 빠르고 작게 해야할 지도 모른다. 모델들을 좀더 작고 빠르게 만들기 위해서 저자들은 간단한 parameter width multiplier $\alpha$를 제시한다. 이 width multiplier $\alpha$는각 레이어에서 균일하게 네트워크를 작게(thin) 해주는 역할을 한다. 이 $\alpha$를 쓰는 방법은 다음과 같다.

어떤 layer가 주어지면, 거기에 Input feature map의 channel M에 곱하고, Output feature map의 channel인 N에도 곱하여서 $\alpha \times M$, $\alpha \times N$을 만들어준다. 그렇게 되면 depthwise separable convolution에 computational cost가 아래 식 4처럼 변한다.

식 4

그럼 Depthwise separable convolution의 연산식을 다음과 같이 쓸 수 있다.

\[D_K \times D_K \times D_F \times D_F \times \alpha \times M + D_{Depth} \times D_{Depth} \times \alpha\times M \times \alpha\times N\]

위 식에서 대략적으로 $\alpha \approx \alpha^2$ 이라고 생각하면 $\alpha^2 \times (D_K \times D_K \times D_F \times D_F \times \times M + D_{Depth} \times D_{Depth} \times \times M \times \times N)$이 되므로, Width mulitplier는 computational cost와, 파라미터의 수를 약 $\alpha^2$ 로 줄여준다. 주의할 점은 accuracy와 latency , size의 trade off를 항상 생각해봐야 한다.

3.4. Resolution Multiplier : Reduced Representation

두번째 hyper-parameter는 네트워크의 computational cost를 줄여주는 것인데,이 것을 resolution multiplier $\rho$라고 한다. resolution multiplier $\rho$은 단순하게 이야기하면 Input image, Input feature map, output of depthwise convolution의 크기를 줄여주는 것이라고 생각하면 된다.

예를 들어, $\rho$ = 0.5 이고, $D_F \times D_F\; =\; 128 \times 128$ 이라면, $\rho\ast D_F \times \rho\ast D_F$ 이런 식으로 사용하여 Input image의 resolution을 낮춰주는 역할을 한다. width multiplier $\alpha$ 와 resolution multiplier $\rho$ 를 computational cost에 곱해주면, 다음과 같이 된다.

\[D_K \times D_K \times \rho \ast D_F \times \rho \ast D_F \times \alpha \ast M + \rho \ast D_{Depth} \times \rho \ast D_{Depth} \times \alpha \ast M \times \alpha \ast N\]

위 식은 결국 아래와 같이 되므로 연산량이 $\rho^2$만큼 줄어들게 된다.

\[\rho^2 \ast (D_K \times D_K \times D_F \times D_F \times \alpha \ast M + D_{Depth} \times D_{Depth} \times \alpha \ast M \times \alpha \ast N)\]

{내 생각에 처음에 Input image를 resize해서 학습하는 것과의 차이는 다음과 같다. 처음에 resize를 통해 입력 이미지의 resolution이 줄어들게 되면, 그대로 계속 convolution이 이어지지만, resolution multiplier ρ 는 각 input들마다 모두 곱해주는 느낌이라서 전체적인 계산량이 줄어든다는 듯 하다. }

테이블 3

테이블 3은 convolution과 Deptwise separable convolution과 각각의 multiplier를 사용했을 때의 연산량, 파라미터의 수를 기록한 것이다. 확실히 multiplier를 사용했을 때, 연산량, 파라미터들이 줄어듦을 확인할 수 있다. { 4번째는 $\alpha$도 적용한 것인지 아닌지 모르겠다.) 그러나, 줄어든다고 해서 무조건 좋은게 아니다. trade off란 항상 존재하기 때문이다.

4. Experiments

---

테이블 4

테이블 4는 같은 MobileNet의 구조를 갖지만, 2번째 row는 Depthwise Separable을 사용한 것이고, ( conv를 depthwise conv -> pointwise conv 로 쪼갬) 1번째 row는 Depthwise Separable을 사용하지않고 그자리에 그냥 conv를 쓴 것인데 정확도는 1%밖에 차이가 나지 않지만, 연산량과 파라미터의 수가 엄청난 차이를 보인다.

테이블 5

테이블 5의 1번째 row는 width multiplier $\alpha = 0.75 $ 를 사용하여 model을 얇게 만든 것이다. 2번째 row는 연산량과 파라미터의 수를 맞추기 위해 MobileNet의 내부의 layer를 제거한 것이다. 결과를 비교해보면 width multiplier $\alpha$ 를 사용하면 layer를 제거하지 않고도 높은 정확도와 적은 연산량, 파라미터 수를 가질 수 있다.

테이블 6

테이블 6는 width multiplier $\alpha$ 를 줄여나가면서 정확도, 계산량, 파라미터의 수를 파악한 것이다. width multiplier $\alpha$ 가 줄어들 때마다, 정확도가 감소하지만 계산량, 파라미터의 수가 대폭 감소하는 것을 확인 할 수 있고 정확도와 (계산량, 파라미터의 수)는 trade off 관계임을 볼 수 있다.

테이블 7

테이블 7는 resolution multiplier $\rho$를 조절해 resolution을 224,192,160,128 순으로 줄이면서 정확도와 계산량, 파라미터의 수를 확인한 것이다. 이 역시 trade off 관계를 가짐을 볼 수 있다.

그러나, resolution multiplier $\rho$는 width multiplier $\alpha$보다 정확도가 좀 더 smooth하게 많은 차이 없이 줄어듦을 볼 수 있다. 따라서 두 파라미터들을 적당하게 사용한다면, 정확도가 비교적 좋으면서 작고 괜찮은 네트워크를 얻어 낼 수 있을 것이다.

테이블 8,9,10

Table 8,9,10은 다른 네트워크들과 비교한 것이다. MobileNet이 정확도 면에서 성능의 부족함을 보이지 않거나 약간 안좋더라도, 연산량이나 파라미터의 수가 어마무시하게 차이가 나는 것을 알 수 있다.

테이블 13

마지막으로 테이블 13을 봐보자. object detection의 수행능력을 나타낸 건인데, 평가 지표는 mAP이다. SSD 300, Faster-RCNN 들의 모델에 VGG, Inception V2, MobileNet을 적용해서 성능을 체크해 봤더니 MobileNet은 성능이 다소 떨어짐을 볼 수 있다. 그러나, 엄청난 계산량의 감소와 말도안되는 파라미터의 감소폭을 볼 수 있었다.

5. 내 생각

그렇게 어렵진 않지만 생각의 전환이 엄청난 효과를 가져오는 것 같다. convolution을 쪼개다니.. 그리고 성능에 대한 트레이드 오프가 있지만 꽤나 흥미로운 논문이었다.