회귀 예측에서 모델링의 중요성

회귀 예측에서 모델링의 중요성

---

회귀 예측에서 예를 들면 우리가 x-t 축으로 이루어진 2차원 그래프를 상상해봅시다. 그리고 x에 따라 다양한 t 값들이 있다고 가정하구요.

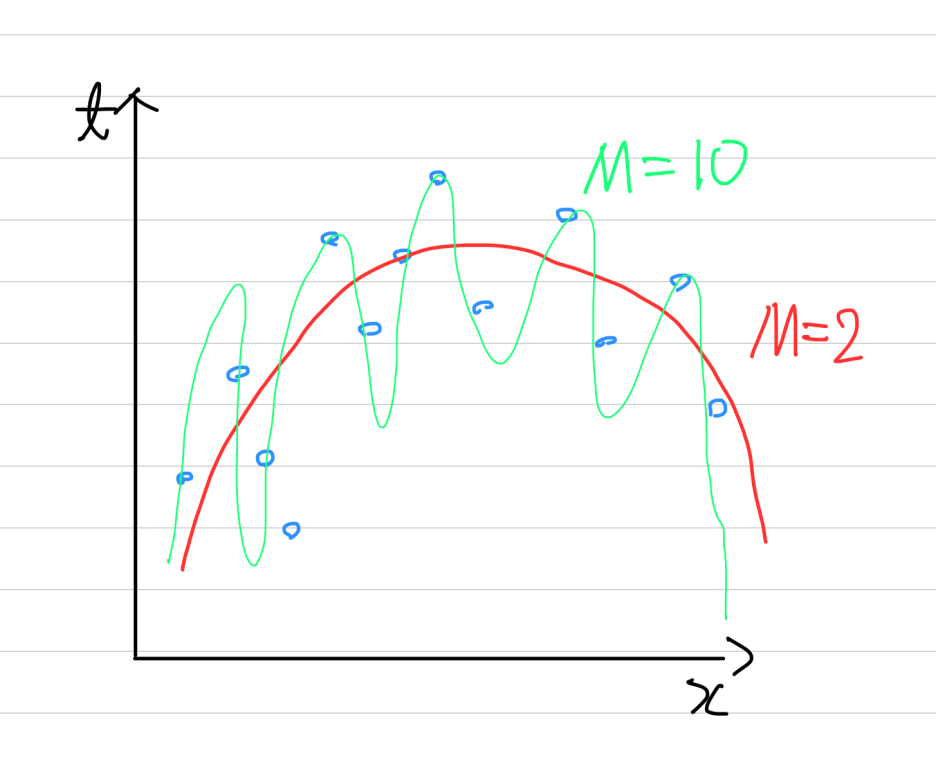
그림 1

그림 1은 데이터에 대해 M차 곡선을 피팅한 모습입니다. M=2일땐 모든 데이터가 맞지 않는 것을 볼 수 있습니다. M=10일땐 많은 데이터들이 딱딱 들어 맞는 것이 보입니다. 실제로 M=10인 모델링을 이용해서 제곱 오차 함수 $J(w)$를 만들어 오차를 측정하면, M=2보다 M=10이 오차가 훨씬 작습니다. 당연히 많은 데이터들이 M=10에 잘 들어맞기 때문이죠.

\[\begin{align*} J(w) = \frac{1}{2}\Sigma^n_{i=1}\{y(x_i,w)-t_i\}^2 \\ y(x_i,w) = w_0+w_1x_1^(i)+...+w_nx_n^(i) \end{align*}\]

※ 여기서 w는 가중치이고 x,t의 아래 첨자 i는 i번째 데이터를 의미합니다.

그러나 오차가 적다고해서, 학습이 잘 됬다고 표현하는 것은 옳지 않습니다. 왜냐하면 학습된 M=10인 모델에 새로운 입력데이터 x를 넣으면 잘못된 예측을 할 확률이 M=2보다 더욱 크기 때문이죠. 데이터의 경향성을 추출하는 것을 실패한 것입니다. 직관적으로도 그림 1을 보면 알 수 있습니다. 우리는 M=10과 같은 경우를 over-fitting 되었다고 말할 수 있습니다. 따라서 모델링이란 것은 머신러닝에 있어서 굉장히 중요한 요소 중 하나입니다.

여기서 만약에 M=10인 모델링을 굳이 사용하겠다고 한다면, 우리는 릿지와 라쏘같은 regularization을 적용함으로써 파라미터 w의 크기 자체를 조정하는 방향으로 회귀 모델링을 수정할 수 있습니다.

개인적인 생각입니다..

---

저는 대학원을 다니면서 프로젝트를 할 때, 데이터를 처리해서 경향을 예측하는 모델을 만드는 프로젝트를 진행한 적이 있었습니다. 그 때 가장 중요하다고 느낀 것은 바로 데이터를 보고 어떤 모델링을 취할 것인가?입니다. 예를 들면, 데이터가 가우시안 분포를 띄는 것 같으면, 가우시안 모델링을 사용해보고자 했습니다. 그래서 프로젝트를 진행할 땐, 항상 데이터의 경향을 분석하고 거기에 맞는 모델링을 해야, 우리는 좋은 모델링을 할 수 있고 좋은 예측을 이끌어 낼 수 있습니다.