Maximum likelihood estimation 사용법
업데이트:
카테고리: 패턴 인식과 머신 러닝
개인적인 생각
개인적으로 우리나라 교육에 아쉬운 점이 있습니다. 해외에서는 어떻게 하는진 모르겠지만.. 대학생 때, 수업을 들으면서 이론들을 대체.. 어디에 어떻게 쓰는지 알려주지 않는 것입니다. 공부라는게 원래 스스로 해야하는 것이긴 하지만.. 솔직히 다들 대학교만 들어가려고 공부해왔지 꿈을 이루려고 들어온 사람이 몇이나 있을까 싶어요.
배우는 이론들이 “어디에 어떻게 어떤 방식으로 적용되는지” 알고 공부했더라면.. 좀 더 공부라는 것을 흥미있게 하지 않았을까 싶습니다..? 누군가는 그건 너가 알아서 해야지라고 할 수 있겠지만, 저는 그게 좀 싫습니다. 스스로 AI관련 공부들을 독학하면서 “누군가가 ‘이것은 말이죠, 이런 경우에 이렇게 쓰이기 때문에 공부를 해야해요~’하면서 길을 알려줬다면, 좀 더 빠르게 이해하거나 흥미를 느끼기 쉽지 않을까”라고 생각합니다. 실제로 이번 글에서 얘기할 가우시안 분포도 이것만 띡 배우면 얘는 실생활에 쓰이지도 않는데.. 누가 재밌게 얘를 공부하겠냐고!!?
이번 포스팅은 가우시안 분포의 파라미터 $\mu$와 $\sigma$가 왜 평균과 표준편차인지, MLE를 사용해서 설명해보려고 합니다. (사실 MLE를 소개하기 위한 글이지만 말이에요 ㅎㅎ)
Gaussian dist와 likelihood의 관계에 대해
이전 글에서 베이지안 이론과 likelihood에 대해 이야기를 했습니다. 이번엔 가우시안 분포와 함께 엮어서 이야기를 해보죠.
가우시안 분포
Gaussian dist는 굉장히 유명한 확률분포입니다. 단일 변수 분포일 땐, 식은 다음과 같습니다.
\[\begin{align*} N(x | \mu,\sigma^2) = \frac{1}{\sqrt{(2\pi\sigma^2)}} exp\{-\frac{(x-\mu)^2}{2\sigma^2}\} \end{align*}\]가우시안에 대한 자세한 이야기는 언급하지 않겠습니다. 여기서 중요한 부분은 파라미터 $\mu,\sigma$입니다. 왜냐하면, 가우시안 분포는 $\mu,\sigma$에 의해서 정해지기 때문이죠.
항상 문제를 해결할 땐, 무엇을 하고싶은지 생각해야합니다!
여기서 우리가 하고싶은 것이 무엇인지 생각하는게 중요합니다. 앞서 얘기한 것처럼, 우리의 목표는 가우시안 분포의 파라미터 $\mu$와 $\sigma$가 왜 평균과 표준편차인지 보는 것입니다.
입력 데이터 x가 N개 있다고 해봅시다. 우리는 입력 데이터를 통해 어떤 확률 분포를 구하고 싶다!라고 생각할 것이고, 확률 분포는 가우시안을 따를 것이다! 라고 가정할 수 있습니다. 예를 들어, 데이터 N개를 그래프로 plotting했더니 ‘어라? 가우시안 분포처럼 생겼는데..?’ 라는 것처럼 말이다.(그냥 제 생각입니다..) 그러면 우리는 다음처럼 식을 구성할 수 있습니다.
\[p(\mu,\sigma^2 | x_i),\;i=1,2,...N\]말로 풀어보면, 데이터들을 보았을 때, $\mu,\sigma$일 확률이라고도 볼 수 있을 것 같네요. 우리가 하고 싶은 것은 데이터를 통해 어떤 확률 분포를 확실히 정하는 것이기 때문에, 위 확률을 최대화하는 것처럼 볼 수 있지 않을까 싶습니다. 즉, 위 확률 값을 최대로!! 만드는 $\mu,\sigma$를 찾고 싶은 것이라는거죠. 근데 우리는 위 식을 수식으로 바로 표현할 수 있을까요?? 저는 못합니다. 저런걸 어떻게 표현하는지 방법조차 모르고요.. 그러나, 이것은 어디선가 많이 본 형태인 걸 알 수 있습니다. 바로 베이지안 이론에서 posterior prob입니다.
\[p(Y | X) = \frac{p(X | Y)p(Y)}{p(X)}\]분모는 정규화항이기 때문에, 우리는 $p(\mu,\sigma^2 | x_i) \propto p(x_i | \mu,\sigma^2)$ 의 식을 얻습니다. 이제 우리의 목표는 자연스레 다음과 같이 바뀝니다.
| **_p(x_i | \mu,\sigma^2)를 최대화 하자!** |
이제 p(x_i | \mu,\sigma^2)에 대해 생각해보죠. 이것은 베이지안 식에서 likelihood에 해당합니다. 그리고 이 형태는 가우시안 식과 똑같죠! 그리고 입력 데이터들이 가우시안 분포를 따르면서 독립적으로 추출되었다고 가정합시다.(naive 가정) 그럼 다음과 같이 식을 적을 수 있습니다.
\[p(x_i | \mu,\sigma^2) = \Pi^N_{i=1}N(x_i | \mu,\sigma^2)\]이제 최종 목표는 다음과 같이 수정됩니다. 위 식, likelihood를 최대화 하는 것이 목표이고, 이것은 흔히 Maximum likelihood (ML) 라고 불리는 것이 됩니다.
Maximum likelihood 푸는 방법
\[p(x_i | \mu,\sigma^2) = \Pi^N_{i=1}N(x_i | \mu,\sigma^2)\]위 식을 최대화하는 $\mu,\sigma$를 어떻게 구할까요? 우선 위 식에 단조증가함수인 log를 씌워봅시다.
\[ln p(x_i | \mu,\sigma^2) = ln \Sigma^N_{i=1}N(x_i | \mu,\sigma^2)\]log를 씌우는 이유는 log가 단조증가함수이므로, 원래 식의 최대값을 찾는 과정이 log의 최대값을 찾는 과정과 같기 때문입니다. 위 식을 전개하면 우리는 아래 식을 얻을 수 있습니다.
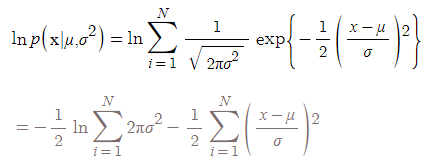
우리는 여기서 $\mu,\sigma$를 찾기 위해, 위 식을 미분하고 극점이 되는 부분을 찾으면 됩니다. 자세한 수식 전개는 직접 해보시길 바랍니다. 직접 해보면 기억에 많이 남기 때문이죠! 전개해보면 우린 다음과 같은 $\mu,\sigma$ 값을 얻을 수 있습니다.
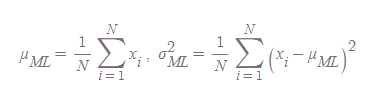
이 결과를 통해서 우리는 가우시안 분포의 $\mu,\sigma$가 왜 평균과 표준편차인지 이해할 수 있게 됩니다.
