논문 공부: Deep Interest Network for Click-Through Rate Prediction(2018)
업데이트:
논문을 읽고 공부하는 글입니다.
해당 분야에 첫 발을 들여놓는 만큼 abstract부터 experiment까지 꼼꼼히 전부 해석하면서 읽고자 합니다.
0. Abstract
이쪽 분야의 딥러닝 기술들은 similar Embedding과 MLP를 사용하는 듯 합니다. 이 방법들은 크기가 큰 scale sparse input feature들을 낮은 차원의 embedding vector들로 매핑하고,
group단위로 고정된 길이의 백터들로 변환됩니다. 마지막으로 이 두개를 결합해 multi-layer perceptron(MLP)으로 보내 feature들 간의 비선형적 관계를 학습합니다.
이 과정 속에서, 사용자의 특징들은 후보 광고군이 무엇이든 상관없이 고정된 길이의 representation vector로 압축됩니다. 사실 이 부분이 bottleneck이 되어 많은 historical behavior들로부터
사용자들의 다양한 어떤 흥미를 효과적으로 팍! 캡쳐하기 위한 Embedding&MLP 방법에 문제를 일으키게 됩니다.
그래서 저자들은 이 모델 Deep Interest Network(DIN)을 제시해 문제를 타파해보려고 합니다. 이 모델은 특정한 광고에 대해 historical behaviors로 부터 사용자 관심도의 representation vector를 배우기 위해 local activation unit을 설계합니다. 이 vector는 다른 광고들에 따라 변화하고, 모델의 표현 능력을 엄청나게 향상시킵니다.
게다가 저자들은 2개의 기술을 개발합니다.
- mini-batch aware regularization
- data adaptive activation function
이것들은 아직은 잘 모르겠지만, 학습할 때 파라미터의 개수에 관련해 영향을 주는 것 같습니다.
데이터 셋으로는 2개의 공공 데이터와 Alibaba real production dataset들을 사용해 저자들의 모델의 효과를 입증하고자 합니다. 실제로 논문이 쓰여질 시점엔 DIN은 이미 알리바바의 online display advertising system에 성공적으로 사용했다고 합니다.
1. Introduction
cost-per-click(CPC) 광고 시스템에서, 광고들은 eCPM(effective cost per mille)에 의해 순위가 매겨집니다. 여기서 eCPM은 입찰 가격과 CTR(click-through rate)의 곱으로 표현됩니다. CTR은 시스템에 의해 예측될 필요가 있습니다. 이런 이유로, CTR 예측 모델의 성능은 최종 수입에 직접적으로 영향을 미치고, 광고 시스템에서 핵심 역할을 맡습니다. CTR 예측을 모델링하는 것은 연구계와 산업계 모두한테 큰 관심사입니다.
최근에, 컴퓨터 비젼과 NLP에서의 딥러닝의 성공으로인해, 딥러닝 기반의 방법들이 CTR을 예측하는 방법에 대한 연구[3,4,21,26]가 발표되고 있습니다. 이 연구들은 similar Embedding&MLP 패러다임을 따릅니다. 이것들은 크기가 큰 scale sparse input feature들을 낮은 차원의 embedding vector들로 매핑하고, group단위로 고정된 길이의 백터들로 변환됩니다. 마지막으로 이 두개를 결합해 multi-layer perceptron(MLP)으로 보내 feature들 간의 비선형적 관계를 학습합니다. 로지스틱 회귀 모델과 비교해서, 위 방법들은 많은 feature engineering job들을 줄일 수 있고, model capability를 크게 향상시킬 수 있습니다. 앞으로 이 논문에선 위 방법들은 간단히 Embedding&MLP라고 부르겠습니다.(이 리뷰 글에선 E&M이라고 하겠습니다.) 이것은 CTR 예측 task에서 요즘(당시에) 가장 인기가 많습니다.
그러나, dimension이 제한된 user presentation vector는 E&M 방법들에서 사용자들의 다양한 interest들을 표현하는데 문제가 될 것입니다(bottleneck). 이커머스 사이트에서 광고를 전시하는 것을 한번 예제로 봅시다. 사용자들은 이커머스 사이트를 방문하고 있을 때, 다른 종류의 물건들을 동시에 관심있게 볼지도 모릅니다. 이것을 user interest들이 다양하다라고 이야기할 수 있습니다. {이 개념은 확실히 알고 갑시다.} CTR 예측 task에 대해선, 사용자의 관심사들(user interests)은 보통 사용자 행동 데이터(user behavior data)로부터 포착됩니다. E&M 방법들은 특정한 사용자들에 대한 모든 관심사들의 representation을 사용자 행동들의 embedding vector들을 고정된 길이의 벡터(fixed-length vector)로 변환하면서 학습합니다. 이 고정된 길이의 벡터는 모든 사용자들의 representation vector들이 표현되는 유클리디안 공간에 있습니다. 다시 말해서, 사용자의 다양한 관심사들은 고정된 길이의 벡터로 압축된다는 것입니다. 고정된 길이의 벡터는 E&M 방법들의 표현 능력을 제한합니다. 그래서! 사용자들의 다양한 관심사들을 충분히 표현해주는 representation capable을 만들기 위해선, 고정된 길이의 벡터의 dimension은 크게 확장될 필요가 있습니다! {표현력을 제한하니까 차원을 키우자는 의미인듯} 그러나.. 불행히도 확장했다가는 학습 파라미터들의 크기도 커질거고 제한된 데이터하에 과적합의 위험성이 커지게 될겁니다. 게다가, 메모리와 계산량에 부담을 주니까 이건 실제 산업현장에서 온라인 시스템으로 사용 할 수 없습니다.
반면에, 후보 광고을 예측할 때, 특정 사용자의 모든 다양한 관심사들을 같은 벡터로 압축할 필요가 없습니다. 왜냐하면, 오직 사용자들의 관심사의 일부분만이 그들이 클릭할지 안할지에 영향을 미치기 때문입니다. 예를 들면, 여성 수영 선수는 저번주에 신발보다 수영복을 샀기 때문에 추천되는 고글을 클릭할 것입니다. 이 것에서 영감을 받아, 저자들은 Deep Interest Network(DIN)이라는 네트워크를 제안합니다! DIN은 후보 광고가 주어진 historical behavior들의 관련성을 고려하면서 사용자 관심사들의 representation vector를 적응적으로(adaptively) 계산합니다. {음.. 직역하면 이런데.. 아마 historical behavior라는 것은 이 사람이 무슨 행동을 해왔는지에 대한 것을 나타내는 것 같습니다. 이 사람이 해온 행동에 따라 후보 광고가 주어져야 이 사람이 클릭하지 않을까요?} local activation unit(?)을 도입함으로써 DIN은 historical behaviors에 관련있는 부분들에 대해 soft-searching하면서 관련된 사용자의 관심사들에 주목하고, 후보 광고에 대한 사용자 관심사들의 representation을 얻기 위해 weighted sum pooling을 합니다. 후보 광고와 높은 관련성을 보이는 behavior들은 아주 활성화된 weight들을 얻고 사용자 관심사들의 representation을 지배합니다. 저자들은 이런 현상을 실험 세션에서 시각화합니다. 이 방법으로 사용자 관심사들의 representation vector는 다른 광고들에 따라 다릅니다. 이것은 제한된 차원에서 모델의 표현 능력을 향상시키고, DIN이 사용자들의 다양한 관심사들을 더 잘 포착하게 해줍니다!
large scale sparse feature들을 가진 산업의 deep network를 학습하는 것은 굉장히 어렵습니다. 예를 들면, SGD 기반의 최적화들은 각 미니 배치에서 나타나는 sparse feature들의 파라미터들만 업데이트합니다. 그러나 전통적인 $L_2$ 정규화를 추가하면, 각 미니 배치에서 모든 파라미터에 대해 $L_2\;norm$을 계산해야해서 계산이 되지 않습니다. (저자들의 경우엔 bilions까지 사이즈 스케일링이 이루어졌다고 합니다..) {sparse feature들에서 업데이트할 필요 없는 0들도 다 업데이트 하니까 차원이 너무 커서 아마 안되는 듯합니다} 본 논문에선, 미니 배치에 나타나는 0이 아닌 feature들에 대해 $L_2\;norm$을 계산해 계산이 되게끔 하는! 새로운 mini-batch aware regularization을 개발합니다. 그리고 입력들의 분포와 관련된 recitified point들을 적응적으로 조정하여 흔히 사용되는 PReLU를 일반화하는 data adaptive activation function를 설계합니다! 이것은 sparse feature들을 갖는 산업 네트워크를 훈련하는데 도움이 될 것입니다.
2. Related work
CTR 예측 모델의 구조는 얕은 것에서부터 깊은 것까지 발전해왔습니다. 동시에, CTR모델에 사용되는 특징들의 차원이나 샘플들(?)의 수는 점점 더 커져갔습니다. 성능을 향상시키기 위해 더 좋은 특징 관계들(feature relations)를 추출하기 위해서, 몇몇 연구들은 모델 구조의 설계에 집중했습니다.
NNLM는 language 모델링에서 차원의 저주를 피하기 위해 각 단어에 대한 distributed representation을 학습합니다. 보통 embedding으로 불리는 이 방법은 large-scale sparse input들을 다루는 많은 NLP 모델들과 CTR 예측 모델들에 영감을 주었습니다. {NNLM은 꼭 읽어봐야 할 것 같습니다. 이번 논문 다음으로 읽읍시다.}
LS-PLM과 FM 모델은 하나의 hidden layer를 가진 네트워크 클래스로 볼 수 있습니다. 이것은 sparse inputs에 embedding layer를 먼저 적용하고난 다음에 target fitting을 위해 특별히 설계된 transformation functions을 부과합니다. 동시에 특징들 사이의 combination relation을 포착하기 위해서 말이죠. {이게 논문을 안 읽어봐서 정확한 내용은 모르겠습니다.}
Deep Crossing, Wide&Deep learning 그리고 유튜브 추천 CTR 모델은 LS-PLM과 FM의 transformation function을 complex MLP network로 바꿈으로써 확장시킵니다. complex MLP network로 바꾸는 것은 model capability를 굉장히 향상시킵니다! PNN은 embedding layer 다음에 product layer를 넣어서 high-order feature interaction을 포착하려 했습니다. {high-order라는건 고차원을 이야기하는건가?} DeepFM은 feature engineering 없이 Wide&Deep에서 “wide” 모듈로서 factorization machine을 사용합니다. 전반적으로 위 방법들은 (sparse한 특징들의 dense representation을 학습하기 위한)embedding layer의 combination와 (특징들의 combination 관계들을 자동으로 학습하는)MLP을 갖는 유사한 모델 구조를 따릅니다. 이런 CTR 예측 모델들은 사람이 직접 feature engineering을 하는 것을 굉장히 줄여줍니다! 그러나 사용자 행동들(user behaviors)이 많은 경우, 특징들은 종종 길이가 변하는 데이터를 가집니다. 예를 들면, 검색된 용어 또는 유튜브 추천 시스템에서 시청된 비디오등이 있습니다. 이런 모델들은 종종 임베딩 벡터들의 일치하는 목록을 sum/average pooling을 통해서 고정된 길이의 벡터로 변환합니다. 단, 이 때 정보 손실을 야기하게 됩니다. 저자들이 제안하는 DIN은 주어진 광고들에 대한 representation 벡터들을 적응적으로 학습함으로써 이런 문제들을 해결합니다. 동시에 모델의 표현 능력또한 상승시키면서 말이죠!
Attention mechanism은 NMT(Neural Machine Translation) 분야로부터 유래됩니다. NMT는 기대되는 annotation을 얻기 위해 모든 annotation의 가중치 합을 얻습니다. 그리고 다음 목표 단어 생성에 관련된 정보에만 오직 집중하죠. Deep intent는 검색 광고의 맥락에 attention을 적용합니다. NMT와 유사하게 이것은 RNN을 모델 텍스트에 사용하고 각각의 쿼리에 핵심 단어들에 집중하게끔 돕는 global hidden vector를 배웁니다. 이것은 attention의 사용이 쿼리 또는 광고의 주요 의도를 포착하는데 도움이 될 수 있다고 보여줍니다. DIN은 관련된 사용자 behavior들에 대한 soft-search를 하기 위한 local activation unit을 설계합니다. 그리고 DIN은 주어진 광고에 관한 사용자 관심도들의 adaptive representation을 얻기 위해 weighted sum pooling을 씁니다. user representation vector는 광고와 사용자간에 상호작용이 없는 DeepIntent와는 다르게, 다른 광고들에 따라 다릅니다.
3. Background
알리바바같은 이커머스 사이트에서, 광고들은 natural goods입니다. {상품이라는 의미일까요?} 앞으로 논문에서 특별한 언급이 없다면, 광고는 상품으로 간주합니다. 그림 1은 알리바바에서 전시 광고 시스템의 과정을 보여줍니다.
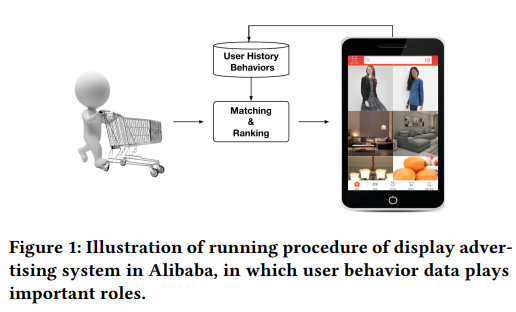 |
|---|
| 그림 1 |
과정은 2가지로 나뉩니다.
- 매칭 스테이지 : collaborative filtering과 같은 방법을 통한 방문한 사용자와 관련된 후보 광고들의 목록을 생성
- 랭킹 스테이지 : 각각의 주어진 광고에 대한 CTR을 예측하고 탑 랭크들을 선택
매일 수 억명이 넘는 사용자들이 이커머스 사이트에 방문하고 많은 사용자 행동 데이터를 남기고 갑니다. 데이터들은 매칭,랭킹 모델들을 만드는게 굉장한 기여를 합니다. {critically라고 써있는데, 아마 긍정적인 의미인듯합니다} 많은 historical hebavior들을 가진 사용자들은 다양한 관심들을 가집니다. 예를 들면, 젊은 엄마들은 울 코드, 티셔츠, 귀거리, 토트백,가죽 핸드백 그리고 아이들의 코트를 최근 많이 검색합니다. 이런 행동 데이터들은 우리에게 그녀들의 쇼핑 관심사들에 대한 힌트를 줍니다. 엄마들이 사이트를 방문했을 때, 시스템은 그녀들에게 적합한 광고를 보여줍니다. 예를 들면 새로운 핸드백같은걸 말이죠. 명백하게 보여진 광고는 이 엄마들의 관심사들과 일치하거나 일부만 활성화(activate)됩니다. 요약하자면, 많은 행동 데이터를 가진 사용자들의 관심사들은 다양하고, 특정 광고가 주어지면 부분적으로 활성화될 수 있습니다. 저자들은 CTR 예측 모델을 짓는데 이런 특성들을 사용하는게 중요하다는 것을 나중에 보여준다고 합니다!
4. Deep Interest Network
Sponsored search와 다르게, 사용자들은 명시적으로 의사를 표현하지 않고 전시 광고 시스템에 들어옵니다. {Sponsored search가 무엇인지 모르겠습니다} CTR 예측 모델을 만들 때, 많은 Historical behavior들로부터 사용자 관심사들을 추출하기 위한 효과적인 접근법이 필요합니다. 사용자들을 묘사하는 특징들과 광고들은 광고 시스템의 CTR 모델링에 있어 기본적인 요소들입니다. 이런 특징들을 합리적으로 사용하고 정보를 추출하는 것은 중요합니다!
4.1. Feature Representation
실제 CTR 예측 task의 데이터는 다음 예제처럼 대부분 다중 그룹 카테고리형(multi-group categorial form)입니다.
- weekday = Friday
- gender = Female
- visited_cate_ids = {Bag,Book}
- ad_cate_id = Book
이 특징들은 인코딩[ 4,19,21]을 통해 고차원의 sparse binary feature로 변환됩니다. 수학적으로 알아야할 개념들에 대해 적어두겠습니다.
- i번째 feature group의 encoding vector : $t_i\;\in\;R^{K_i}$. $K_i$은 feature group i의 차원이고, feature group i은 $K_i$ 유일한 광고들을 포함을 의미함. {$K_i$ unique ads가 무엇인지 아직 모르겠습니다.}
- $t_i[j]$ : $t_i$의 j번째 요소, 이것은 0 또는 1의 값을 가지며 $\Sigma_{j=1}^{K_i} t_i[j]=k$를 만족함.
- if $k=1$, one-hot encoding이고, else if $k>1$, multi-hot encoding이다. {one-hot은 벡터 하나에 1이 한개인 것이고, multi-hot은 2개 이상인 것을 얘기합니다.}
- 1개의 인스턴스 예시 : $x\;=\;[t_1^T,…,t_2^T,t_M^T]^T$. M은 feature 그룹들의 수이고 $\Sigma_{i=1}^{M} K_i=K$를 만족함. $K$는 전체 feature space의 차원.
이 방식으로 이번 세션 4.1의 시작에서 얘기했던 예제를 수학적으로 표현해보면 다음과 같습니다.
- weekday = Friday -> [0,0,0,0,1,0,0] {아마 월,화,수,목,금,토,일 을 binary로 표현한 것 같네요.}
- gender = Female -> [0,1] {성별에는 남,여 밖에 없습니다.}
- visited_cate_ids = {Bag,Book} -> [0, … , 1, … , 1, … , 0] {다른 항목들이 무엇이 더 있는지 모르는 상황이므로 Bag,Book에만 1이 되어있는 모습입니다.}
- ad_cate_id = Book -> [0, … , 1, … , 0] {위 상황과 동일합니다.}
저자들의 시스템에서 전체 feature set은 테이블 1과 같이 표현됩니다.
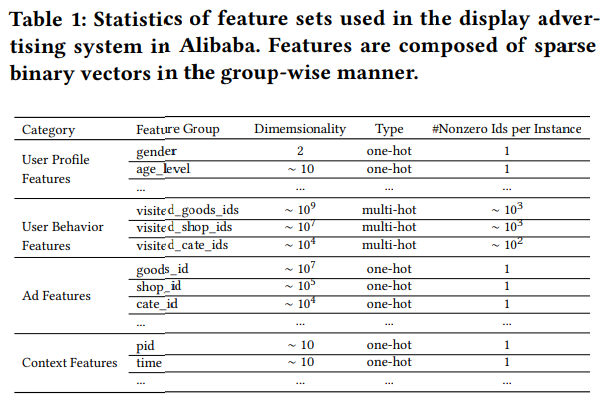 |
|---|
| 테이블 1 |
보면 4개의 카테고리로 구성되어있고, user behavior features는 전형적인 multi-hot encoding 벡터들이고, 사용자 관심사들의 많은 정보를 포함합니다. 여기서 저자들은 combination feature들을 사용하지 않았음을 알아야합니다. 저자들은 deep neural network로 특징들의 interaction을 포착할 것이기 때문에 그런 것 같네요!?
4.2. Base Model(Embedding&MLP)
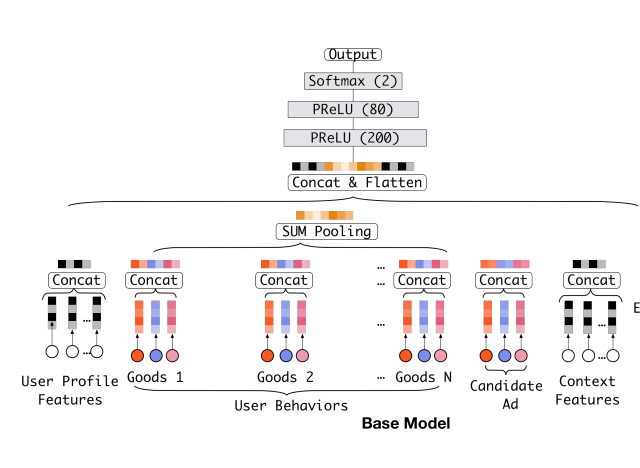 |
|---|
| 그림 2. Base model |
가장 인기있는 모델 구조[3,4,21]는 그림 2처럼 유사한 Embedding&MLP paradigm을 가집니다. 저자들은 이 모델을 DIN의 base model로 사용한다고 하네요. 저자들의 DIN의 구조는 그림 3과 같습니다.
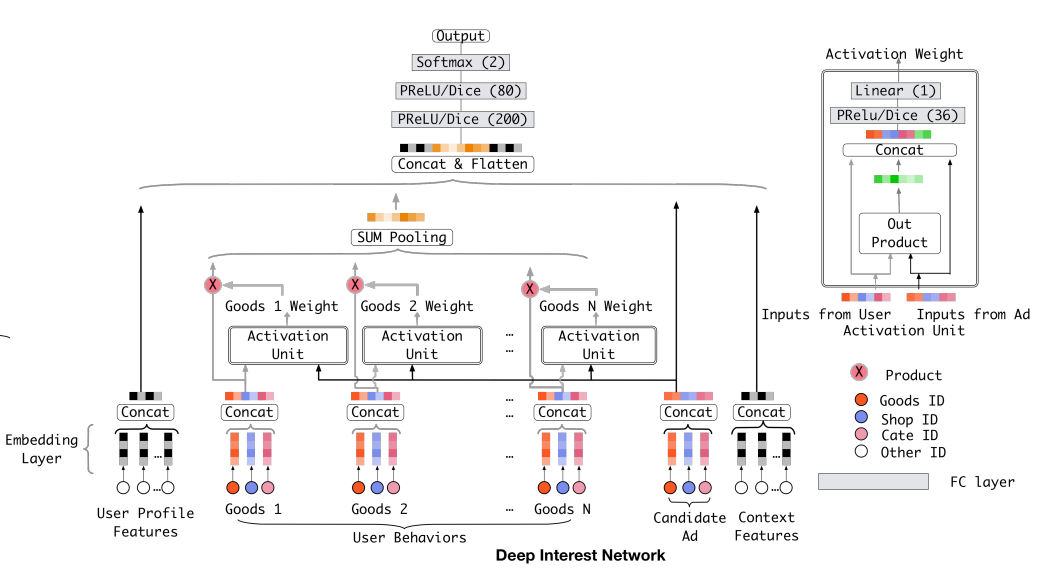 |
|---|
| 그림 3. Deep Interest Network |
Embedding layer
입력 데이터들이 고차원의 binary 벡터들이라서 이것을 저차원의 dense representation으로 변환하기 위해서 embedding layer를 사용한다고 합니다. i번째 feature 그룹 $t_i$에 대해, i번째 embedding dictionary를 $W^i=[w_1^i,…,w_j^i,…,w_{K_i}^i]\;\in\;R^{D\times K_i}$라고 표현합니다. $w_j^i\in R^D$는 D차원의 embedding vector라고 합니다. Embedding operation은 table lookup 메커니즘을 따른다는데.. 이게 뭔진 잘 모르겠네요.
- 만약 원-핫 벡터 $t_i$라면 j번째 요소가 $t_i[j]=1$가 됩니다. 그럼 $W^i$와 $t_i$가 곱해지면 $w_j^i$만 남습니다. 이걸 single embedding vector $e_i$라고 합니다
- 만약 멀티-핫 벡터 $t_i$라면 j번째 요소는 여전히 $t_i[j]=1$이지만, $j\in {i_1,i_2,…,i_k}$ k개의 1이 있을 겁니다. 그럼 $t_i$의 embedded representation은 리스트처럼 뽑혀서 single embedding vector $e_{i_k}$들이 묶인 ${ e_{i_1},e_{i_2},…,e_{i_k} }={ w^i_{i_1},w^i_{i_2},…,w^i_{i_k}}$가 됩니다.
Pooling layer and Concat layer
사용자마다 행동의 수가 다릅니다. 그래서 멀티-핫 behavioral feature vector $t_i$의 0이 아닌 값의 수는 데이터마다 다르죠. 이것은 embedding 벡터들의 리스트의 길이를 다양하게 만듭니다. fully connected network은 오직 고정된 길이의 입력들만 다룰 수 있기에, embedding 벡터들의 리스트를 pooling layer를 통해 고정된 길이의 벡터로 바꿔야합니다.
\[e_i=pooling(e_{i_1},e_{i_2},...,e_{i_k})\]가장 많이 사용되는 pooling layer들은 sum pooling과 average pooling입니다. 전자는 embedding vector들의 리스트를 element-wise sum을 하고, 후자는 평균을 계산하죠.
embedding과 pooling layer들은 원래의 sparse한 feature들을 여러개의 고정된 길이의 representation vector들로 매핑하는 group-wise 방식으로 작동합니다. {아마 함께 작동한다는 느낌인 것 같습니다.} 그러면 모든 벡터들은 전체적인 representation 벡터를 얻기위해 함께 concatenate됩니다.
MLP
앞서 concatanated된 dense representation 벡터가 주어지면, fully connected layer들은 feature들의 조합을 자동으로 학습하곤 합니다. 최근에 발전된 방법[4,5,10]은 더 나은 정보 추출을 위해서 MLP의 구조를 설계했죠.
Loss
base모델에 사용된 목적함수는 다음과 같은 negative log-likelihood 함수입니다.
\[L=-\frac{1}{N}\sum_{(x,y)\in S} (y\log p(x) + (1-y)\log (1-p(x)))\]※ $S$는 N개의 학습 셋을 얘기하고, $x$는 입력 데이터, $y$는 0 또는 1을 갖는 이진 label입니다. 그리고 $p(x)$는 softmax layer를 통해 얻는 sample $x$가 클릭 될 것으로 예측되는 확률입니다.
4.2. The structure of Deep Interest Network
테이블 1의 feature들에서, 사용자 행동 feature들은 중요하고 사용자 관심도를 모델링하는데 핵심 역할을 합니다.
Base model는 앞선 방법으로 사용자 관심도에 대한 고정된 길이의 representation vector를 얻습니다. 이 representation vector는 어떤 후보 광고든 상관 없이 주어진 사용자에 대해 같음을 유지합니다. 그래서 제한된 dimension을 갖는 사용자 representation vector는 사용자의 다양한 관심사들을 표현하기 하는데에 bottleneck이 됩니다. 이걸 해결하기 위한 간단한 방법은 embedding vector의 차원을 확장하는거지만.. 이렇게하면 learning parmameter의 크기가 매우 커질 것입니다. 그렇게 되면 제한된 학습 데이터에서 overfitting이 일어날 것이고, 용량과 계산량에 부담을 줘서 산업의 online system에선 쓸 수 없게되죠.
그럼 어떻게 이 문제를 해결해야할까요!? 사용자 관심사들의 local activation 특성은 우리에게 Deep Interset Network를 만들 수 있게 영감을 줍니다! 챕터3에서 젊은 엄마의 예시를 들었는데, 기억하시나요? 그녀는 보여지는 새로운 핸드백을 찾고 클릭합니다. click action의 추진력을 해부해 봅시다! 전시된 광고는 그녀의 과거의 행동들을 soft-searching하고 최근에 토트백과 가죽 핸드백과 비슷한 물건을 검색했던 것을 찾아서 젊은 엄마의 관련된 관심사들을 hit! 합니다. 즉, 전시된 광고와 관련된 행동들은 click action에 매우 영향을 주죠. 그래서 DIN은 주어진 광고에 관한 locally activated interest의 representation에 주목하면서 이 과정을 시뮬레이션합니다. 모든 유저들의 다양한 관심도들을 같은 벡터로 표현하는 것 대신에, DIN은 후보 광고에 대한 과거 행동의 관련성을 고려하여 사용자 관심도의 representation 벡터를 적응적으로 계산합니다.
그림 3은 DIN의 구조를 나타냅니다. Base model과 비교하면 DIN은 local activation unit을 소개하고 다른 틀은 같습니다. 특히, activation unit들은 사용자 behavior feature들에 적용됩니다. 이것은 주어진 후보 광고 A에 대한 사용자 representation $\nu_U$을 적응적으로 계산하기 위해 weighted sum pooling을 수행합니다.
\[\nu_U(A) = f(\nu_A,e_1,e_2,...,e_H) = \sum^H_{j=1}a(e_j,\nu_A)e_j =\sum^H_{j=1}w_je_j\]※ ${e_1,e_2,…,e_H}$는 사용자 U의 길이가 H인 embedding vector list를 의미하고, $\nu_A$는 광고 A의 embedding vector입니다. 이 방법으로 $\nu_U(A)$는 다른 광고들마다 바뀝니다. $a(\ast)$는 그림 3에서 Goods N Weight라고 써있는 activation weight를 출력하는 feed-forward 네트워크입니다. 그리고 $a(\ast)$는 이들의 out product를 더한다는데.. 이게 그림이랑 엮어서 봐도 무슨 소린지 아직 모르겠습니다.
local activation unit은 NMT에서 개발된 attention method와 비슷한 아이디어입니다. 그러나 다른 점은 constraint $\sum_i w_i=1$이 사용자 관심도의 intensity를 보존하는 것을 목표로 하면서 $\nu_U(A)$ 계산을 느슨하게 해준다는 겁니다. 이전의 방법에선 $a(\ast)$의 출력에 softmax로 normalization을 하는데, 이걸 대신해서 contraint를 거는 것 같네요.
예를 들어봅시다. 한 사용자의 과거 행동들이 90%는 옷, 10%는 전자기기를 포함하면, 티셔츠와 핸드폰의 두 광고가 주어졌을 때, 티셔츠 광고는 clothes에 속한 과거 행동의 대부분에 작용해서 아마 $\nu_U$가 핸드폰보다 가장 큰 값을 가질 겁니다. 기존의 방법은 이런 resolution을 잃는다고 하네요.
저자들은 LSTM도 써보려했지만, 그리 좋은 결과를 얻진 못했나봅니다.
5. Training Techniques
이번엔 알리바바에서 대용량의 데이터들을 가지고 학습할 때 도움이 되는 2개의 기술들에 대해 소개하네요.
5.1. Mini-batch Aware Regularization
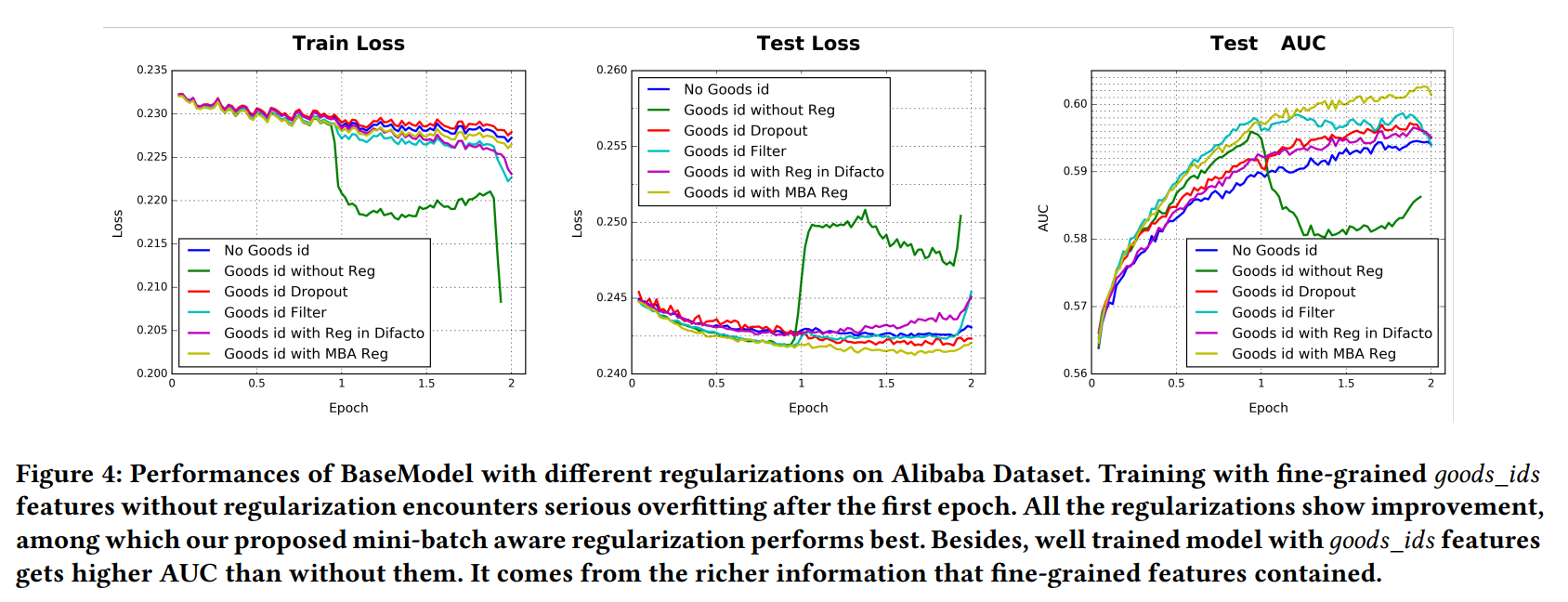 |
|---|
| 그림 4 |
Overfitting은 큰 문제죠. 예를 들어, 테이블 1에서 사용자의 visited_goods_ids와 광고의 goods_id를 포함한 0.6 billion의 차원을 갖는 goods_ids의 feature같은 경우, 모델의 성능을 regularization없이 첫 epoch만에 급격히 떨어뜨립니다. 그림 4에서 어두운 초록색 라인처럼 말이죠. 그렇다고 직접 전통적인 regularization을 적용해 버리는 것도 실용적인 방법은 아닙니다(릿지,라쏘 같은 규제말이죠). 정말일까요?
한번 릿지 규제 $l_2\;regularization$을 예로 들어봅시다. 규제 없이 SGD를 베이스로 하는 최적화 방법에서는 오직 각각의 mini-batch에서 나타나는 0이 아닌 sparse feature들만 필요합니다. 그러나 릿지 규제를 추가하면, 각각의 mini-batch마다 모든 파라미터들(가중치 같은)에 대해 L2 norm을 계산해야합니다. 왜냐하면, 릿지 규제는 파라미터(가중치)의 절대값을 최대한 작게 만드는게 목표이기 때문이죠. 그래서 너무 많은 계산이 필요하게 되니까.. 문제가 발생합니다.
이 논문에서 효과적인 mini-batch aware regularizer를 소개합니다. 이건 각각의 미니 배치에서 나타나는 sparse feature들의 파라미터들에 대해 L2 norm을 계산합니다. 사실, embedding dictionary가 CTR 네트워크의 대부분의 파라미터들에 기여하고 많은 계산량의 어려움을 유발합니다. $W \in R^{D\times K}$는 전체 embedding dictionary의 파라미터들을 얘기합니다. D는 임베딩 벡터의 차원이고, K는 feature space의 차원입니다. $W$에 대한 릿지 규제를 확장해봅시다.
\[L_2(W) = || W ||_2^2 = \sum_{j=1}^K || w_j ||^2_2 = \sum_{(x,y)\in S} \sum_{j=1}^K \frac{I(x_j \neq 0)}{n_j} || w_j ||^2_2\]- $w_j \in R^D$ : j번째 임베딩 벡터
- $I(x_j \neq 0)$ : 데이터 객체 x가 feature id $j$를 갖는지 여부
- $n_j$ : 모든 샘플들에서 feature id $j$가 발생하는 횟수
{위 식처럼 되는 이유를 제 생각대로 설명해보겠습니다. K차원을 갖는 데이터 객체 $x$가 N개 있다고 한다면, $X\in R^{N\times K}$가 됩니다. 데이터 객체 벡터 $x$는 원-핫/멀티-핫 인코딩으로 이루어져있기 때문에, j번째 요소에는 0또는 1이 있겠죠. 그럼 j번째 column에는 N개의 요소들이 있는데, 그 중 1인 것들의 수를 세어 $n_j$를 만드는 겁니다. 그렇게 되면 위 식의 제일 마지막 항의 첫 summation과 I()와 $n_j$가 이해가 될겁니다. $x$의 j번째 요소가 0이 아닌 것은 $n_j$만큼 있으니 상수항으로 곱해져도 결국 같은 식이 되는겁니다. }
위 식은 mini-batch를 이용한 식으로 다음과 같이 바꿀 수 있습니다.
\[L_2(W) = \sum_{j=1}^K \sum_{m=1}^B \sum_{(x,y)\in B_m} \frac{I(x_j \neq 0)}{n_j} || w_j ||^2_2\]- $B$ : 미니 배치의 수
- $B_m$ : m번째 미니 배치
미니 배치 $B_m$에서 feature id j를 갖는 데이터가 하나라도 있는지 묻는 $\alpha_{mj}=\max_{(x,y)\in B_m} I(x_j \neq 0)$을 설정합시다. 아마 미니배치 $B_m$에서 j번째 요소에 1인 값의 수를 표현하는 것 같네요?
그러면 위 식은 다음과 근사화할 수 있습니다.
\[L_2(W) \approx \sum_{j=1}^K \sum_{m=1}^B \frac{\alpha_{mj}}{n_j} || w_j ||^2_2\]m번째 미니베치에서, feature j의 embedding weights에 대한 gradient는 다음과 같습니다.
\[w_j \leftarrow w_j-\eta [\frac{1}{ | B_m | } \sum_{(x,y)\in B_m} \frac{\partial L(p(x),y)}{\partial w_j}+\lambda \frac{\alpha_{mj}}{n_j}w_j]\]5.2. Data Adaptive Activation Function
 |
|---|
| 그림 3 |
PReLU는 다음과 같습니다.
\[f(s) = \begin{cases} s,\;\text{if}\;s>0 & \\ \alpha s ,\; \text{if}\;s <= 0 \end{cases} = p(s) \cdot s + (1-p(s)) \cdot \alpha s\]$s$는 활성화함수 $f(\cdot)$의 1차원 입력이고, $p(s)=I(s>0)$은 $f(s)$를 $s와 \alpha s$로 스위칭 해주는 indicator 함수입니다. $\alpha$는 학습파라미터이구요. 그림 3의 왼쪽은 제어함수로써의 PReLU를 보여줍니다. PReLU는 0에서 급격한 변화를 보입니다. 이것은 각각의 레이어의 입력들이 다른 분포를 따를 때, 적절하지 않을 것입니다. 이것을 고려해서, 저자들은 새로운 data adaptive activation function을 그림 3의 오른쪽처럼 설계하고 _Dice_라고 이름 짓습니다. 식은 다음과 같습니다.
\[f(s) = p(s) \cdot s + (1-p(s)) \cdot \alpha s, \; p(s) = \frac{1}{1+e^{-\frac{s-E[s]}{\sqrt{\text{Var}[s]+\epsilon}}}}\]학습 페이즈에서, $E[s]$와 $\text{Var}[s]$ 는 각각의 미니 배치에서 입력의 평균과 분산입니다. 테스트 페이즈에서, $E[s]$와 $\text{Var}[s]$ 는 데이터에 대한 평균 $E[s]$와 $\text{Var}[s]$ 를 움직이면서..? 계산됩니다. { 이게 무슨소린진 아직 모르겠네요 } $\epsilon$은 작은 상수로 $10^{-8}$로 잡았다고 합니다.
Dice는 PReLU의 일반화로 보여질 수 있습니다. 핵심은 입력 데이터의 분포에 따라 recitified point를 adaptively하게 조정한다는 것입니다. 게다가, Dice는 스위칭하는데 스무스하게 사용하구요. $E[s]$와 $\text{Var}[s]$ 가 0일땐, Dice는 PReLu에서 degenerate하다고 합니다..?
6. Experiments
{이제 실험파트입니다! 결과가 궁금하네요!}
6.1. Datasets and Experimental Setup
데이터 셋은 다음의 3가지를 사용합니다.
- Amazon dataset
- MovieLens dataset
- Alibaba dataset
데이터 셋의 통계는 테이블 2와 같습니다. 자세한 설명은 논문을 참고해주세요.
 |
|---|
| 테이블 2 |
6.2. Competitors
비교에 사용되는 모델들은 다음의 5가지 입니다.
*LR : CTR 예측 태스크를 위한 딥 네트워크들이 있기 전에 널리 사용되던 얕은 모델
- BaseModel : 4.2에서 소개했던 Embedding&MLP 구조를 갖는 모델입니다.
- Wide&Deep : 실제 산업 현장에서 사용되는 모델입니다. 자세한 내용은 논문을 참고합시다.
- PNN : BaseModel에서 조금 향상된 모델입니다.
- DeepFM : Wide&Deep에 “wide” 모듈로써 feature engineering job을 저장하는 factorization machine을 넣은 모델입니다.
6.3. Metrics
평가 지표로 user weighted AUC를 사용합니다.
\[AUC = \frac{\sum_{i=1}^n #\text{impression}_i \times AUC_i}{\sum_{i=1}^n #\text{impression}_i}\]그리고 모델들에 대한 상대적인 향상치를 측정하기 위해 RelaImpr 평가 지표를 도입합니다.
\[\text{RelaImpr} = (\frac{AUC(measured model)-0.5}{AUC(BaseModel)-0.5}-1)\times 100%\]여기서 BaseModel의 정확도를 기준으로 삼는걸 볼 수 있네요!
6.4. Result from model comparison on Amazon dataset dan MovieLens dataset
 |
|---|
| 테이블 3 |
테이블 3은 각 데이터 셋들에 대한 결과를 보여줍니다. 각 실험들은 5번 반복해서 평균낸 것입니다. DIN이 가장 성능이 좋지만, 특히 사용자 행동 데이터가 굉장히 많은 아마존데이터셋에서 엄청난 성능을 보여줍니다! 저자들은 이 결과의 공을 local activation unit structure로 돌리네요.
6.5. Performance of reqularization
 |
|---|
| 그림 4 |
 |
|---|
| 테이블 4 |
사실, MovieLens와 아마존 데이터셋의 feature의 차원이 그리 크지 않아서 저자들이 생각하던 overfitting 문제를 제대로 만나지 못했다고 합니다. 알리바바의 데이터셋은 엄청 차원이 커서, overfitting문제를 만났다고 하네요. 어떤 규제도 걸지 않고 overfitting문제를 만나게 되면, 그림 4의 어두운 초록색 선처럼 epoch 1부터 모델의 성능이 급격히 떨어집니다. 그래서 저자들은 다음의 4가지의 규제 방식으로 각각 실험해서 차이를 확인해보려고합니다.
- Dropout
- Filter
- Regularization in DiFacto : feature들과 자주 관련되는 파라미터들의 지나친 규제를 줄입니다.?
- MBA : 저자들이 제안하는 방법입니다.
그림 4와 테이블 4는 결과를 보여줍니다.
- Dropout : overfitting을 꽤 막아주지만, 수렴이 느리군요.
- Filter : Dropout과 비슷해 보입니다.
- DiFacto : 이것은 goods_id가 높은 빈도 수를 보이기에, 패널티를 주었습니다. 그래서 filter보다 더 안좋은 것 같네요?
저자들의 방법은 다른 방법들에 비해 상당히 overfitting 문제를 막아줍니다.
